
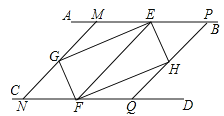
【题目】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
(1)求证:四边形EGFH是矩形;
(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.

【答案】(1)证明见试题解析;(2)答案不唯一,例如:FG平分∠CFE;GE=FH;∠GME=∠FQH;∠GEF=∠EFH.
【解析】
试题分析:(1)利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠GEH=90°,进而求出四边形EGFH是矩形;
(2)利用菱形的判定方法首先得出要证MNQP是菱形,只要证MN=NQ,再证∠MGE=∠QFH得出即可.
试题解析:(1)∵EH平分∠BEF,∴∠FEH=![]() ∠BEF,∵FH平分∠DFE,∴∠EFH=
∠BEF,∵FH平分∠DFE,∴∠EFH=![]() ∠DFE,∵AB∥CD,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=
∠DFE,∵AB∥CD,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=![]() (∠BEF+∠DFE)=
(∠BEF+∠DFE)=![]() ×180°=90°,∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°﹣(∠FEH+∠EFH)=180°﹣90°=90°,同理可得:∠EGF=90°,∵EG平分∠AEF,∴∠EFG=
×180°=90°,∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°﹣(∠FEH+∠EFH)=180°﹣90°=90°,同理可得:∠EGF=90°,∵EG平分∠AEF,∴∠EFG=![]() ∠AEF,∵EH平分∠BEF,∴∠FEH=
∠AEF,∵EH平分∠BEF,∴∠FEH=![]() ∠BEF,∵点A、E、B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,∴∠FEG+∠FEH=
∠BEF,∵点A、E、B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,∴∠FEG+∠FEH=![]() (∠AEF+∠BEF)=
(∠AEF+∠BEF)=![]() ×180°=90°,即∠GEH=90°,∴四边形EGFH是矩形;
×180°=90°,即∠GEH=90°,∴四边形EGFH是矩形;
(2)答案不唯一:由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,
要证MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,
故只要证GM=FQ,即证△MGE≌△QFH,易证 GE=FH、∠GME=∠FQH.
故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N。
(1)求△AEN的周长;
(2)求证:BE=EN=NC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为![]() ,所以
,所以![]() 从而
从而![]() (当a=b时取等号).
(当a=b时取等号).
阅读2:若函数![]() ;(m>0,x>0,m为常数),由阅读1结论可知:
;(m>0,x>0,m为常数),由阅读1结论可知:![]() ,所以当
,所以当![]() ,即
,即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() .
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为![]() ,周长为2(
,周长为2(![]() ),求当x= 时,周长的最小值为 ;
),求当x= 时,周长的最小值为 ;
问题2:已知函数![]() (
(![]() )与函数
)与函数![]() (
(![]() ),
),
当x= 时,![]() 的最小值为 ;
的最小值为 ;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com