练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．抛物线经过A（-1，0），B（3，0），过（0，-2）点的直线l与x轴平行，抛物线与直线l有交点，结合函数图象，求a的取值范围．

    分析 求得对称轴，如果过（0，-2）点的直线l与x轴平行，抛物线与直线l有交点，则开口向上，当顶点为（1，-2）时求得a的值，即可求得a的取值．

    解答 解：∵物线经过A（-1，0），B（3，0），
    ∴对称轴x=$\frac{-1+3}{2}$=1，
    当抛物线的顶点为（1，-2）时，则y=a（x-1）2-2，
    代入（-1，0）得，4a-2=0，
    解得a=$\frac{1}{2}$，
    所以过（0，-2）点的直线l与x轴平行，抛物线与直线l有交点，则a的取值范围为a≥$\frac{1}{2}$．

    点评 本题考查了二次函数图象上点的坐标特征，求得顶点为（1，-2）时的a的值是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．计算：-3-|-2|-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．为了在校体育节的排球比赛上取得好成绩，甲、乙、丙、丁四人一起训练传接球．传接球规则如下：接球者把球随机传给另外三人中的一人．现由甲开始传球，请回答下列问题（假设每次传球都能接到球）：
    （1）写出第一次接球者是乙的概率；
    （2）用列表或画树状图的方法求第二次接球者是甲的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，一个长方形运动场被分隔成A、B、A、B、C共5个区，A区是边长为am的正方形，C区是边长为bm的正方形．
    （1）列式表示每个B区长方形场地的周长，并将式子化简；
    （2）列式表示整个长方形运动场的周长，并将式子化简；
    （3）如果a=20，b=10，求整个长方形运动场的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

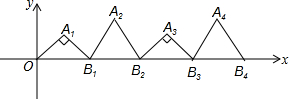    4．如图，在平面直角坐标系的第一象限内，依次作等腰直角三角形OA1B1，正三角形B1A2B2，等腰直角三角形B2A3B3，…，且∠A1=∠A3=∠A5=…=90°，B1坐标为（2，0），B2坐标为（4，0），B3坐标为（6，0），…，按这样的规律，点A2015的坐标是（　　）
    A．（4029，1）B．（2015，$\sqrt{3}$）C．（4030，1）D．（4029，$\sqrt{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，已知△ABC中，中线BD⊥AB，AB=6，BD=4，求tan∠CBD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）-23+（π-3.14）0+|1-2$\sqrt{3}$|-$\sqrt{12}$
    （2）$\sqrt{27}$×$\sqrt{\frac{2}{3}}$+（$\sqrt{2}$-1）2
    （3）解方程组$\left\{\begin{array}{l}{x+2y=3①}\\{3x-4y=4②}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若$\frac{4a}{4-|a|}$有意义，则$\frac{4a}{4-a}$的值（　　）
    A．无意义B．有意义C．值为0D．以上答案都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如果在Rt△ABC中，∠C=90°，AC=2，BC=3，那么下列各式正确的是（　　）
    A．tanB=$\frac{2}{3}$B．cotB=$\frac{2}{3}$C．sinB=$\frac{2}{3}$D．cosB=$\frac{2}{3}$

    查看答案和解析>>

    同步练习册答案