
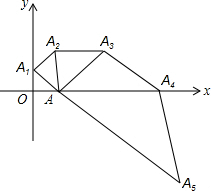
 如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰直角三角形AA1A2,再以Rt△AA1A2的斜边AA2为直角边,画第三个等腰直角气角形AA2A3…依此类推,则点A2016的坐标是(-21008+1,0).
如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰直角三角形AA1A2,再以Rt△AA1A2的斜边AA2为直角边,画第三个等腰直角气角形AA2A3…依此类推,则点A2016的坐标是(-21008+1,0). 分析 根据等腰直角三角形的斜边长为直角边长度的$\sqrt{2}$倍,可以根据规律发现第n个直角三角形的斜边长,再根据点A2016的位置即可求出其坐标.
解答 解:∵△OAA1是腰长为1的等腰直角三角形,
∴第一个直角三角形的斜边长:1×$\sqrt{2}$=$\sqrt{2}$,
∵以Rt△OAA1的斜边AA1为直角边,画第二个等腰直角三角形AA1A2,
∴第二个三角形的斜边长:1×$\sqrt{2}$×$\sqrt{2}$=($\sqrt{2}$)2,
同理可得,第三个三角形的斜边长:1×$\sqrt{2}$×$\sqrt{2}$×$\sqrt{2}$=($\sqrt{2}$)3,
…
以此类推,第n个三角形的斜边长为:($\sqrt{2}$)n,
∴第2016个等腰直角三角形的斜边长是:($\sqrt{2}$)2016,
∵A8在x轴的负半轴上,2016÷8=252,
∴A2016在x轴的负半轴上,且A2016O=A2016A-OA=21008-1,
∴点A2016的坐标是(-21008+1,0).
故答案为:(-21008+1,0).
点评 此题主要考查了等腰直角三角形的性质的运用,解答此题的关键是通过认真分析,根据等腰直角三角形的斜边长为直角边长度的 $\sqrt{2}$倍,从中发现规律.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 2个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图数轴上表示的是下列哪个不等式组的解集( )
如图数轴上表示的是下列哪个不等式组的解集( )| A. | $\left\{\begin{array}{l}x>-2\\ x≤3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x≥-2\\ x<3\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<-2\\ x≥3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x≤-2\\ x>3\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
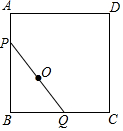 如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.
如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com