
【题目】如图所示,AB是⊙O的直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
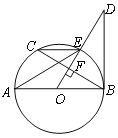
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
【答案】(1)答:BD和⊙O相切.
证明:∵OD⊥BC,
∴∠OFB=∠BFD =90°,
∴∠D+∠3=90°.
∵∠4=∠D=∠2, ……………………………1分
∴∠2+∠3=90°,
∴∠OBD=90°,
即OB⊥BD.
∵点B在⊙O上,
∴BD和⊙O相切. ……………………………2分
(2) ∵OD⊥BC,BC=8,
∴BF="FC=4. " ……………………………3分
∵ AB=10,
∴OB=OA=5.
在Rt△OFB中, ∠OFB =90°,
∵OB=5,BF=4,
∴OF="3. " ……………………………4分
∴tan∠1=![]() .
.
在Rt△OBD中, ∠OBD =90°,
∵tan∠1=![]() , OB=5,
, OB=5,
∴![]() . …………………………… 5分
. …………………………… 5分
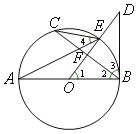
【解析】试题分析:(1)因为同弧所对的圆周角相等,所以有∠AEC=∠ABC,又∠AEC=∠ODB,所以∠ABC=∠ODB,OD⊥弦BC,即∠ABC+∠BOD=90°,则有∠ODB+∠BOD=90°,即BD垂直于AB,所以BD为切线.
(2)连接AC,由于AB为直径,所以AC和BC垂直,又由(1)知∠ABC=∠ODB,所以有△ACB∽△OBD,而AC可由勾股定理求出,所以根据对应线段成比例求出BD.
试题解析:(1)答:BD和⊙O相切.
证明:∵OD⊥BC,
∴∠OFB=∠BFD=90°,
∴∠D+∠3=90°.
∵∠4=∠D=∠2,
∴∠2+∠3=90°,
∴∠OBD=90°,
即OB⊥BD.
∵点B在⊙O上,
∴BD和⊙O相切.
(2)∵OD⊥BC,BC=8,
∴BF="FC=4"
∵AB=10,
∴OB=OA=5.
在Rt△OFB中, ∠OFB =90°,
∵OB=5,BF=4,
∴OF=3.
∴tan∠1=![]() .
.
在Rt△OBD中, ∠OBD =90°,
∵tan∠1=![]() , OB=5,
, OB=5,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】⊙O的半径为5cm,A是线段OP的中点,当OP=7cm时,点A与⊙O的位置关系是( )
A. 点A在⊙O内B. 点A在⊙O上C. 点A在⊙O外D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
已知:△ABC是任意三角形.
(1)如图1所示,点M、P、N分别是边AB、BC、CA的中点.求证:∠MPN=∠A.
(2)如图2所示,点M、N分别在边AB、AC上,且![]() ,
, ![]() ,点P1、P2是边BC的三等分点,你认为∠MP1N+∠MP2N=∠A是否正确?请说明你的理由.
,点P1、P2是边BC的三等分点,你认为∠MP1N+∠MP2N=∠A是否正确?请说明你的理由.

(3)如图3所示,点M、N分别在边AB、AC上,且![]() ,
, ![]() ,点P1、P2、……、P2009是边BC的2010等分点,则∠MP1N+∠MP2N+……+∠MP2009N=____________.
,点P1、P2、……、P2009是边BC的2010等分点,则∠MP1N+∠MP2N+……+∠MP2009N=____________.
(请直接将该小问的答案写在横线上.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每位同学都能感受到日出时美丽的景色.下图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com