
某移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;“神舟行”不缴月租费,每通话1min付费0.6元.若一个月内通话x min,两种方式的费用分别为y1元和y2元.
(1)写出y1、y2与x之间的函数关系式;
(2)一个月内通话多少分钟,两种移动通讯费用相同;
(3)你能为用户设计一个方案,使用户合理地选择通信业务吗?
(4)某人估计一个月内通话300min,应选择哪种移动通讯合算些.
(1)y1=50+0.4x;y2=0.6x;(2)250;(3)方案见解析;(4)全球通.
解析试题分析:(1)因为移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;“神舟行”不缴月租费,每通话1min付费0.6元.若一个月内通话xmin,两种方式的费用分别为y1元和y2元,则y1=50+0.4x,y2=0.6x;
(2)令y1=y2,解方程即可;
(3)分三种情况设计方案.
(4)令x=300,分别求出y1、y2的值,再做比较即可.
试题解析:(1)y1=50+0.4x;y2=0.6x;
(2)令y1=y2,则50+0.4x=0.6x,
解之,得x=250
所以通话250分钟两种费用相同;
(3)令y1>y2,则50+0.4x>0.6x,
解之,得x<250
所以通话少于250分钟选择神舟行合算;
令y1<y2,则50+0.4x<0.6x,
解之,得x>250
所以通话超过250分钟选择全球通合算;
(4)因为300>250,所以选择全球通合算。
考点:一次函数的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1•k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y= x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.


(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲、乙两车分别从A地将一批物品运往B地,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的数据回答:
(1)甲车出发多长时间后被乙车追上?
(2)甲车与乙车在距离A地多远处迎面相遇?
(3)甲车从B地返回的速度多大时,才能比乙车先回到A地?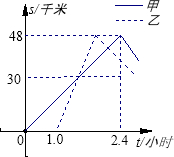
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数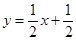 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数
的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数 的表达式.
的表达式. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知等腰△AOB放置在平面直角坐标系xOy中, OA=OB,点B的坐标为(3,4) .
(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数 (x>0)的图象上.
(x>0)的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售, 售出土豆千克数与他手中持有的钱(含备用零钱)的关系如图所示,结合图象回答下列问题: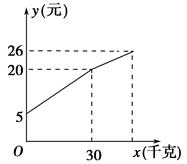
(1) 农民自带的零钱是多少?
(2) 降价前他每千克土豆出售的价格是多少?
(3) 降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱) 是26元,问他一共带了多少千克土豆.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y=kx+b与反比例函数 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b> 的解集______________;
的解集______________;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com