
【题目】如图,在△ABC中,BC>AC , 点D在BC上,且DC=AC , ∠ACB的平分线CF交AD于F , 点E是AB的中点,连接EF . 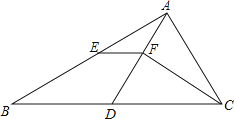
(1)求证:2EF=BD ,
(2)四边形BDFE的面积为6,求△ABD的面积.
【答案】
(1)解答:∵DC=AC,CF为∠ACB的平分线,
∴AF=DF,
∵AE=EB,AF=DF,
∴EF为△ABD的中位线,
∴2EF=BD.
(2)解答:∵EF为△ABD的中位线,
∴EF∥BD,2EF=BD,
∴△AEF∽△ABD
∴两三角形相似比K=1:2,
∴ =K2= ,
则4(S△ABD-6)=S△ABD,
解得:S△ABD=8.
【解析】分析:(1)根据等腰三角形性质推出F为AD中点,根据三角形的中位线定理推出即可;(2)根据三角形中位线推出EF∥BD , 推出△AEF∽△ABD且两三角形相似比K=1:2,得出面积比是 ![]() ,代入求出即可.
,代入求出即可.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上). 
(1)若以C、E、F为顶点的三角形与以A、B、C为顶点的三角形相似. ①当AC=BC=2时,AD的长为;
②当AC=3,BC=4时,AD的长为;
(2)当点D是AB的中点时,△CEF与△CBA相似吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段d是线段a、b、c的第四比例项,其中a=2cm,b=4cm,c=5cm,则d等于( ).
A.1cm
B.10cm
C.2.5cm
D.1.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为CD上一点,连接AE、BD , 且AE、BD交于点F , DE:EC=2:3,则S△DEF:S△ABF=( ) 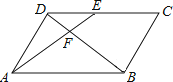
A.2:3
B.4:9
C.2:5
D.4:25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=![]() ,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.
,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为6cm , 7.5cm , 9cm , △DEF的一边长为4cm , 当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm
B.4 cm,5 cm
C.5 cm,6 cm
D.6 cm,7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D , 与AB及AC的延长线分别交于E , F , 写出图中的一对全等三角形是 ;一对相似三角形是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF. 
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com