
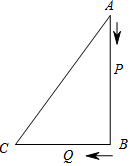
 ��ͼ����֪��ABC�У���B=90�㣬AB=12cm��BC=9cm��P��Q�ǡ�ABC���ϵ��������㣬���е�P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊÿ��1cm����Q�ӵ�B��ʼ��B��C��A�����˶������ٶ�Ϊÿ��2cm������ͬʱ�������������ʱ��Ϊt�룮
��ͼ����֪��ABC�У���B=90�㣬AB=12cm��BC=9cm��P��Q�ǡ�ABC���ϵ��������㣬���е�P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊÿ��1cm����Q�ӵ�B��ʼ��B��C��A�����˶������ٶ�Ϊÿ��2cm������ͬʱ�������������ʱ��Ϊt�룮���� ��1����ȷ����BP��BQ���ٸ��ݹ��ɶ������ɵó����ۣ�
��2�������AC�����жϳ����������ĵ�Q����AC�ϣ��ٷ�����������ۼ��㼴�ɣ�
��3����������ó���P��Q���˶�·����������ε��ܳ��������ڻ����ܵ��ϵ�ͬ���˶�����
��� �⣺��1�����˶�֪��AP=1��BQ=2��1=2��
��AB=12��
��BP=12-t=11��
��Rt��PBQ�У����ݹ��ɶ����ã�PQ=$\sqrt{B{P}^{2}+B{Q}^{2}}$=5$\sqrt{5}$��
��2����Rt��ABC�У����ݹ��ɶ����ã�AC=15��
�ߡ�QCB�ǵ��������Σ�
���Q����AC�ϣ�
��QB=QCʱ����Q��AC���е㣬
��t=��BC+$\frac{1}{2}$AC����2=��9+7.5����2=8.25�룬
��CQ=CB=9ʱ��t=��BC+CQ����2=��9+9����2=9�룬
��BQ=BCʱ����ͼ��
����B��BD��AC��D��
��CQ=2CD��
��Rt��ABC�У�S��ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•BD��
��BD=$\frac{AB•BC}{AC}$=$\frac{12��9}{15}$=$\frac{36}{5}$��
��Rt��BCD�У����ݹ��ɶ������ã�CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\frac{27}{5}$��
��CQ=2CD=$\frac{54}{5}$��
��t=��BC+CQ����2=9.9�룬
��������8.25���9���9.9��ʱ����QCB�ǵ��������Σ�
��3��������֪��2t-t=AB+BC+AC=12+9+15��
��t=36��
��������36�룬P��Q��һ��������
���� �������������ۺ��⣬��Ҫ�����˹��ɶ��������������ε����ʣ������ε������ʽ���⣨1���Ĺؼ������BP���⣨2���Ĺؼ����жϳ���Q���ڱ�AC�ϣ��⣨3���Ĺؼ��ǵó���P��Q���˶�·����������ε��ܳ�����һ��������Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
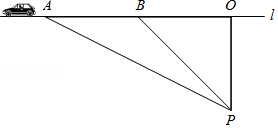 ��ͨ��ȫ������ע���ȵ����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ���꼶��ѧ�С���ͬѧ�����˲��������ٶȵ�ʵ�飮��ͼ�����ڱ�ֱ�Ĺ�·1��ѡȡһ��P���ڹ�·1��ȷ����O��B��ʹ��PO��l��PO=100�ף���PBO=45�㣮��ʱ��һ���γ��ڹ�·1����B��A����ʻ������ô˳���B����ʻ��A�����õ�ʱ��Ϊ3�룬����á�APO=60�㣮��·������ÿСʱ80ǧ�ף����жϴ˳��Ƿ��٣���˵�����ɣ��ο����ݣ�$\sqrt{2}$=1.41��$\sqrt{3}$=1.73����
��ͨ��ȫ������ע���ȵ����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ���꼶��ѧ�С���ͬѧ�����˲��������ٶȵ�ʵ�飮��ͼ�����ڱ�ֱ�Ĺ�·1��ѡȡһ��P���ڹ�·1��ȷ����O��B��ʹ��PO��l��PO=100�ף���PBO=45�㣮��ʱ��һ���γ��ڹ�·1����B��A����ʻ������ô˳���B����ʻ��A�����õ�ʱ��Ϊ3�룬����á�APO=60�㣮��·������ÿСʱ80ǧ�ף����жϴ˳��Ƿ��٣���˵�����ɣ��ο����ݣ�$\sqrt{2}$=1.41��$\sqrt{3}$=1.73�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
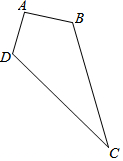 ������ĸ�ľ����β�����������������ݶ����ӣ����ܹ���һ��ƽ��ͼ�Σ�
������ĸ�ľ����β�����������������ݶ����ӣ����ܹ���һ��ƽ��ͼ�Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͬλ����� | |
| B�� | ƽ����ͬһֱ�ߵ���ֱ��ƽ�� | |
| C�� | ��ͬһƽ���ڣ���һ����ֻ��һ��ֱ������ֱ֪�ߴ�ֱ | |
| D�� | ��ֱ��ƽ�У��ڴ������ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com