
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
①当x取什么值时,y>0 ?
②当x取什么值时,y的值随x的增大而减小?
(1) ;(2)(-1,0),(3,0);(3)图象见解析;(4)①-1<x<3,②x≥1.
;(2)(-1,0),(3,0);(3)图象见解析;(4)①-1<x<3,②x≥1.
解析试题分析:(1)将(0,3)代入y=-x2+(m-1)x+m求得m,即可得出抛物线的解析式;
(2)令y=0,求得与x轴的交点坐标;令x=0,求得与y轴的交点坐标;
(3)得出对称轴,顶点坐标,画出图象即可;
(4)①当y>0时,即图象在一、二象限内的部分;②在对称轴的右侧,y的值随x的增大而减小.
试题解析:(1)∵抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点,∴m=3.
∴抛物线的解析式为 .
.
(2)令y=0,得 ,解得x=-1或3.
,解得x=-1或3.
∴抛物线与x轴的交点坐标(-1,0),(3,0);
(3)对称轴为x=1,顶点坐标(1,4),图象如图:
(4)如图,①当-1<x<3时,y>0.
②当x≥1时,y的值随x的增大而减小.
考点:1.抛物线与x轴的交点2.;二次函数的图象;3.曲线上点的坐标与方程的关系.


科目:初中数学 来源: 题型:解答题
已知抛物线y=x²-4x+3.
(1)该抛物线的对称轴是 ,顶点坐标 ;
(2)将该抛物线向上平移2个单位长度,再向左平移3个单位长度得到新的二次函数图像,请写出相应的解析式,并用列表,描点,连线的方法画出新二次函数的图像;
| x | … | | | | | | … |
| y | … | | | | | | … |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为 米,面积为
米,面积为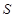 平方米.(注:
平方米.(注: 的近似值取3)
的近似值取3)
(1)求出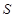 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)当半径 为何值时,扇形花坛的面积最大,并求面积的最大值.
为何值时,扇形花坛的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,抛物线 与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
锐角△ABC中,BC=6, ,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
(1)求△ABC中边BC上高AD;
(2)当x为何值时,PQ恰好落在边BC上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.
(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com