
ЎҫМвДҝЎҝ¶ФУЪЖҪГжЙПAЎўBБҪөгЈ¬ёшіцИзПВ¶ЁТеЈәТФөгAОӘЦРРДЈ¬BОӘЖдЦРТ»ёц¶ҘөгөДХэ·ҪРОіЖОӘөгAЎўBөДЎ°БмУтЎұЈ®
ЈЁ1Ј©ТСЦӘөгAөДЧшұкОӘЈЁ©Ғ1Ј¬1Ј©Ј¬өгBөДЧшұкОӘЈЁ3Ј¬3Ј©Ј¬¶ҘөгAЎўBөДЎ°БмУтЎұөДГж»эОӘЎЎ ЎЎЈ®
ЈЁ2Ј©ИфөгAЎўBөДЎ°БмУтЎұөДХэ·ҪРОөДұЯУлЧшұкЦбЖҪРР»тҙ№ЦұЈ¬»ШҙрПВБРОКМвЈә
ўЩТСЦӘөгAөДЧшұкОӘЈЁ2Ј¬0Ј©Ј¬ИфөгAЎўBөДЎ°БмУтЎұөДГж»эОӘ16Ј¬өгBФЪxЦбЙП·ҪЈ¬ЗуBөгЧшұкЈ»
ўЪТСЦӘөгAөДЧшұкОӘЈЁ2Ј¬mЈ©Ј¬ИфФЪЦұПЯlЈәyЈҪ©Ғ3x+2ЙПҙжФЪөгBЈ¬өгAЎўBөДЎ°БмУтЎұөДГж»эІ»і¬№э16Ј¬ЦұҪУРҙіцmөДИЎЦө·¶О§Ј®
Ўҫҙр°ёЎҝЈЁ1Ј©40Ј»ЈЁ2Ј©ўЩBЈЁ4Ј¬2Ј©»тBЈЁ0Ј¬2Ј©Ј»ўЪ©Ғ12ЎЬmЎЬ4Ј®
ЎҫҪвОцЎҝ
ЈЁ1Ј©УЙБҪөгҫаА빫КҪҝЙЗуABіӨЈ¬УЙХэ·ҪРОөДРФЦКҝЙЗуҪвЈ»
ЈЁ2Ј©ўЩ·ЦБҪЦЦЗйҝцЈ¬УЙБҪөгҫаА빫КҪәНХэ·ҪРОРФЦКҝЙЗуҪвЈ»
ўЪУЙМвТвҝЙөГBMЈҪAMЈ¬ҝЙөГmЈҪ4©Ғ4aЈ¬»тmЈҪ©Ғ2aЈ¬УЙХэ·ҪРОөДРФЦКҝЙЗуaөДИЎЦө·¶О§Ј¬јҙҝЙЗуҪвЈ®
ЈЁ1Ј©ЎЯөгAөДЧшұкОӘЈЁ©Ғ1Ј¬1Ј©Ј¬өгBөДЧшұкОӘЈЁ3Ј¬3Ј©Ј¬
ЎаABЈҪ![]() Ј¬
Ј¬
УЙМвТвҝЙЦӘЈ¬ABКЗХэ·ҪРО¶ФҪЗПЯөДТ»°лЈ¬
ЎаХэ·ҪРОөДұЯіӨОӘ2![]() Ј¬
Ј¬
ЎаХэ·ҪРОөДГж»эОӘ40Ј¬
Ўа¶ҘөгAЎўBөДЎ°БмУтЎұөДГж»эОӘ40Ј»
№Кҙр°ёОӘ40Ј»
ЈЁ2Ј©ўЩИзНјЈ¬
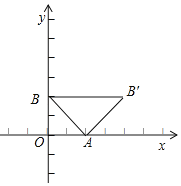
ЎЯөгAЎўBөДЎ°БмУтЎұөДХэ·ҪРОөДұЯУлЧшұкЦбЖҪРР»тҙ№ЦұЈ¬
ЎаABУлxЦбөДЛщіЙИсҪЗОӘ45ЎгЈ¬
өұөгBФЪAЧуІаЈ¬ЙиBЈЁ2©ҒaЈ¬aЈ©Ј¬
ЎаABЈҪ![]() Ј¬
Ј¬
ЎЯөгAЎўBөДЎ°БмУтЎұөДГж»эОӘ16Ј¬
Ўа16ЈҪ![]() Ј¬
Ј¬
ЎаaЈҪ2Ј¬
ЎаөгBЈЁ0Ј¬2Ј©Ј¬
өұөгBФЪөгAУТІаЈ¬ЙиB'ЈЁ2+aЈ¬aЈ©
ЎаAB'ЈҪ![]() aЈ¬
aЈ¬
ЎЯөгAЎўBөДЎ°БмУтЎұөДГж»эОӘ16Ј¬
Ўа16ЈҪ![]() Ј¬
Ј¬
ЎаaЈҪ2Ј¬
ЎаөгBЈЁ4Ј¬2Ј©Ј¬
ЧЫЙПЛщКцЈәBЈЁ4Ј¬2Ј©»тBЈЁ0Ј¬2Ј©Ј»
ўЪИзНј2Ј¬№эөгBЧчBMЎНAMЈ¬
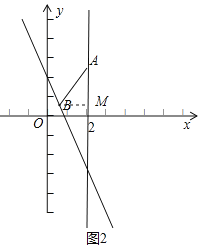
ЎЯЎЯөгAЎўBөДЎ°БмУтЎұөДХэ·ҪРОөДұЯУлЧшұкЦбЖҪРР»тҙ№ЦұЈ¬
ЎаABУлЦұПЯxЈҪ2өДЛщіЙИсҪЗОӘ45ЎгЈ¬
ЎаBMЈҪAMЈ¬
ЙиөгBЈЁaЈ¬©Ғ3a+2Ј©Ј¬
ЎаAMЈҪ|m+3a©Ғ2|Ј¬BMЈҪ|2©Ғa|
ЎаABЈҪ![]() |2©Ғa|Ј¬
|2©Ғa|Ј¬
ЎЯөгAЎўBөДЎ°БмУтЎұөДГж»эІ»і¬№э16Ј¬
Ўа![]() ЎЬ16
ЎЬ16
Ўа0ЎЬaЎЬ4Ј¬
ЎЯBMЈҪAMЈ¬
Ўа|m+3a©Ғ2|ЈҪ|2©Ғa|
ЎаmЈҪ4©Ғ4aЈ¬»тmЈҪ©Ғ2aЈ¬
Ўа©Ғ12ЎЬmЎЬ4Ј¬»т©Ғ8ЎЬmЎЬ0Ј¬
ЧЫЙПЛщКцЈә©Ғ12ЎЬmЎЬ4Ј®


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘУӯҪУ2020ДкЦРҝјЈ¬ДіЦРС§¶ФИ«РЈҫЕДкј¶С§ЙъҪшРРБЛТ»ҙОКэС§ЖЪД©ДЈДвҝјКФЈ¬ІўЛж»ъійИЎБЛІҝ·ЦС§ЙъөДІвКФіЙјЁЧчОӘСщұҫҪшРР·ЦОцЈ¬»жЦЖіЙБЛИзПВБҪ·щІ»НкХыөДНіјЖНјЈ¬ЗлДгёщҫЭНіјЖНјЦРМṩөДРЕПўҪвҙрПВБРОКМвЈә
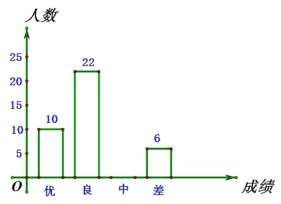
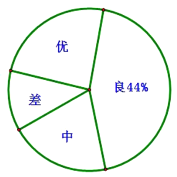
ЈЁ1Ј©ФЪХвҙОөчІйЦРЈ¬Т»№ІөчІйБЛ¶аЙЩГыС§ЙъЈ»
ЈЁ2Ј©Ҫ«МхРОНіјЖНјІ№ідНкХыЈ»
ЈЁ3Ј©ИфёГЦРС§ҫЕДкј¶№ІУР860ИЛІОјУБЛХвҙОКэС§ҝјКФЈ¬№АјЖёГРЈҫЕДкј¶№ІУР¶аЙЩГыС§ЙъөДКэС§іЙјЁҝЙТФҙпөҪУЕРгЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
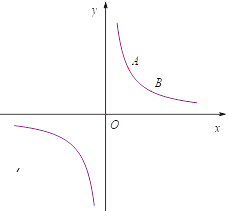
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ТСЦӘ![]() өгөДәбЧшұкОӘ2Ј¬Ҫ«
өгөДәбЧшұкОӘ2Ј¬Ҫ«![]() өгПтУТЖҪТЖ2ёцөҘО»Ј¬ФЩПтПВЖҪТЖ2ёцөҘО»өГөҪ
өгПтУТЖҪТЖ2ёцөҘО»Ј¬ФЩПтПВЖҪТЖ2ёцөҘО»өГөҪ![]() өгЈ¬ЗТ
өгЈ¬ЗТ![]() Ўў
Ўў![]() БҪөгҫщФЪЛ«ЗъПЯ
БҪөгҫщФЪЛ«ЗъПЯ![]() ЙПЈ®
ЙПЈ®
ЈЁ1Ј©Зу·ҙұИАэәҜКэөДҪвОцКҪЈ®ЈЁ2Ј©ИфЦұПЯ![]() УЪ·ҙұИАэәҜКэ
УЪ·ҙұИАэәҜКэ![]() өДБнТ»Ҫ»өгОӘ
өДБнТ»Ҫ»өгОӘ![]() Ј¬Зу
Ј¬Зу![]() өДГж»эЈ®
өДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЧЫәПУлМҪҫҝ:
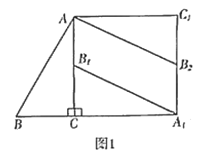
![]() ІЩЧч·ўПЦ:ИзНј1Ј¬ФЪ
ІЩЧч·ўПЦ:ИзНј1Ј¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬ТФөг
Ј¬ТФөг![]() ОӘЦРРДЈ¬°С
ОӘЦРРДЈ¬°С![]() ЛіКұХлРэЧӘ
ЛіКұХлРэЧӘ![]() Ј¬өГөҪ
Ј¬өГөҪ![]() ;ФЩТФөг
;ФЩТФөг![]() ОӘЦРРДЈ¬°С
ОӘЦРРДЈ¬°С![]() ДжКұХлРэЧӘ
ДжКұХлРэЧӘ![]() Ј¬өГөҪ
Ј¬өГөҪ![]() .Б¬ҪУ
.Б¬ҪУ![]() .Фт
.Фт![]() Ул
Ул![]() өДО»ЦГ№ШПөОӘЖҪРРЈ»
өДО»ЦГ№ШПөОӘЖҪРРЈ»
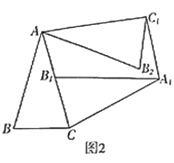
![]() МҪҫҝЦӨГч:ИзНј2Ј¬өұ
МҪҫҝЦӨГч:ИзНј2Ј¬өұ![]() КЗИсҪЗИэҪЗРОЈ¬
КЗИсҪЗИэҪЗРОЈ¬![]() КұЈ¬Ҫ«
КұЈ¬Ҫ«![]() °ҙХХЈЁ1Ј©ЦРөД·ҪКҪЈ¬ТФөг
°ҙХХЈЁ1Ј©ЦРөД·ҪКҪЈ¬ТФөг![]() ОӘЦРРДЈ¬°С
ОӘЦРРДЈ¬°С![]() ЛіКұХлРэЧӘ
ЛіКұХлРэЧӘ![]() Ј¬өГөҪ
Ј¬өГөҪ![]() Ј»ФЩТФөг
Ј»ФЩТФөг![]() ОӘЦРРДЈ¬°С
ОӘЦРРДЈ¬°С![]() ДжКұХлРэЧӘ
ДжКұХлРэЧӘ![]() Ј¬өГөҪ
Ј¬өГөҪ![]() .Б¬ҪУ
.Б¬ҪУ![]() Ј¬
Ј¬
ўЩМҪҫҝ![]() Ул
Ул![]() өДО»ЦГ№ШПөЈ¬РҙіцДгөДМҪҫҝҪбВЫЈ¬ІўјУТФЦӨГчЈ»
өДО»ЦГ№ШПөЈ¬РҙіцДгөДМҪҫҝҪбВЫЈ¬ІўјУТФЦӨГчЈ»
ўЪМҪҫҝ![]() Ул
Ул![]() өДО»ЦГ№ШПөЈ¬РҙіцДгөДМҪҫҝҪбВЫЈ¬ІўјУТФЦӨГч.
өДО»ЦГ№ШПөЈ¬РҙіцДгөДМҪҫҝҪбВЫЈ¬ІўјУТФЦӨГч.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ЦұПЯlЈәyЈҪkx+1ЈЁkЎЩ0Ј©УлЦұПЯxЈҪkЈ¬ЦұПЯyЈҪ©Ғk·ЦұрҪ»УЪөгAЎўBЈ¬ЦұПЯxЈҪkУлЦұПЯyЈҪ©ҒkҪ»УЪөгCЈ¬
ЈЁ1Ј©ЗуЦұПЯlУлyЦбөДҪ»өгЧшұкЈ»
ЈЁ2Ј©әбЎўЧЭЧшұк¶јКЗХыКэөДөгҪРЧцХыөгЈ®јЗПЯ¶ОABЎўBCЎўCAО§іЙөДЗшУтЈЁІ»ә¬ұЯҪзЈ©ОӘWЈ®
ўЩөұkЈҪ1КұЈ¬ЗшУтДЪөДХыөгУРЎЎ ЎЎёцЈ¬ЖдЧшұкОӘЎЎ ЎЎЈ®
ўЪөұkЈҪ2КұЈ¬ЗшУтWДЪөДХыөгУРЎЎ ЎЎёцЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘәлСпЦР»Әҙ«НіОД»ҜЈ¬ЗӯДПЦЭҪьЖЪҫЩ°мБЛЦРРЎС§ЙъЎ°№ъС§ҫӯөдҙуИьЎұЈ®ұИИьПоДҝОӘЈәAЈ®МЖК«Ј»BЈ®ЛОҙКЈ»CЈ®ВЫУпЈ»DЈ®ИэЧЦҫӯЈ®ұИИьРОКҪ·ЦЎ°өҘИЛЧйЎұәНЎ°Л«ИЛЧйЎұЈ®
ЈЁ1Ј©РЎАцІОјУЎ°өҘИЛЧйЎұЈ¬ЛэҙУЦРЛж»ъійИЎТ»ёцұИИьПоДҝЈ¬ЗЎәГійЦРЎ°ИэЧЦҫӯЎұөДёЕВККЗ¶аЙЩЈҝ
ЈЁ2Ј©РЎәмәНРЎГчЧйіЙТ»ёцРЎЧйІОјУЎ°Л«ИЛЧйЎұұИИьЈ¬ұИИь№жФтКЗЈәН¬Т»РЎЧйөДБҪГы¶УФұөДұИИьПоДҝІ»ДЬПаН¬Ј¬ЗТГҝИЛЦ»ДЬЛж»ъійИЎТ»ҙОЈ¬ФтЗЎәГРЎәмійЦРЎ°МЖК«ЎұЗТРЎГчійЦРЎ°ЛОҙКЎұөДёЕВККЗ¶аЙЩЈҝЗлУГ»ӯКчЧҙНј»тБРұнөД·Ҫ·ЁҪшРРЛөГчЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
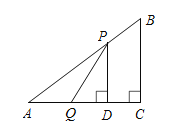
ЎҫМвДҝЎҝИзНјЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .өг
.өг![]() УЙөг
УЙөг![]() іц·ўСШ
іц·ўСШ![]() ·ҪПтПтөг
·ҪПтПтөг![]() ФИЛЩФЛ¶ҜЈ¬Н¬Кұөг
ФИЛЩФЛ¶ҜЈ¬Н¬Кұөг![]() УЙөг
УЙөг![]() іц·ўСШ
іц·ўСШ![]() ·ҪПтПтөг
·ҪПтПтөг![]() ФИЛЩФЛ¶ҜЈ¬ЛьГЗөДЛЩ¶ИҫщОӘ
ФИЛЩФЛ¶ҜЈ¬ЛьГЗөДЛЩ¶ИҫщОӘ![]() .Чч
.Чч![]() УЪ
УЪ![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() Ј¬ЙиФЛ¶ҜКұјдОӘ
Ј¬ЙиФЛ¶ҜКұјдОӘ![]() Ј¬ҪвҙрПВБРОКМвЈә
Ј¬ҪвҙрПВБРОКМвЈә
ЈЁ1Ј©Йи![]() өДГж»эОӘ
өДГж»эОӘ![]() Ј¬Зу
Ј¬Зу![]() Ул
Ул![]() Ц®јдөДәҜКэ№ШПөКҪЈ¬
Ц®јдөДәҜКэ№ШПөКҪЈ¬![]() өДЧоҙуЦөКЗ Ј»
өДЧоҙуЦөКЗ Ј»
ЈЁ2Ј©өұ![]() өДЦөОӘ КұЈ¬
өДЦөОӘ КұЈ¬![]() КЗөИСьИэҪЗРО.
КЗөИСьИэҪЗРО.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДҫ№ӨКҰёөҝЙТФУГҪЗіЯІвБҝІўјЖЛгіцФІөД°лҫ¶rЈ®УГҪЗіЯөДҪП¶МұЯҪфҝҝЎСOЈ¬ҪЗіЯөД¶ҘөгBЈЁЎПBЈҪ90ЎгЈ©Ј¬ІўК№ҪПіӨұЯУлЎСOПаЗРУЪөгCЈ®

ЈЁ1Ј©ИзНјЈ¬ABЈјrЈ¬ҪП¶МұЯABЈҪ8cmЈ¬¶БөГBCіӨОӘ12cmЈ¬ФтёГФІөД°лҫ¶rОӘ¶аЙЩЈҝ
ЈЁ2Ј©Из№ыABЈҪ8cmЈ¬јЩЙиҪЗіЯөДұЯBCЧг№»іӨЈ¬Иф¶БөГBCіӨОӘacmЈ¬ФтУГә¬aөДҙъКэКҪұнКҫrОӘЎЎ ЎЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
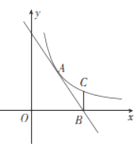
ЎҫМвДҝЎҝИзНјЈ¬·ҙұИАэәҜКэy=![]() (x>0)УлЦұПЯABҪ»УЪөгA(2Ј¬3)Ј¬ЦұПЯABУлxЦбҪ»УЪөгB(4Ј¬0)Ј¬№эөгBЧчxЦбөДҙ№ПЯBCҪ»·ҙұИАэәҜКэөДНјПуУЪөгCЈ¬ФЪЖҪГжДЪУРөгDЈ¬К№өГТФAЈ¬BЈ¬CЈ¬DЛДөгОӘ¶ҘөгөДЛДұЯРООӘЖҪРРЛДұЯРОЈ¬ФтЖҪРРЛДұЯРОABCDөДГж»эОӘ____________Ј®
(x>0)УлЦұПЯABҪ»УЪөгA(2Ј¬3)Ј¬ЦұПЯABУлxЦбҪ»УЪөгB(4Ј¬0)Ј¬№эөгBЧчxЦбөДҙ№ПЯBCҪ»·ҙұИАэәҜКэөДНјПуУЪөгCЈ¬ФЪЖҪГжДЪУРөгDЈ¬К№өГТФAЈ¬BЈ¬CЈ¬DЛДөгОӘ¶ҘөгөДЛДұЯРООӘЖҪРРЛДұЯРОЈ¬ФтЖҪРРЛДұЯРОABCDөДГж»эОӘ____________Ј®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com