正三角形的半径R＝1，则它的边心距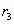
＝________，边长
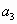＝________，高h＝________．
开心蛙状元测试卷系列答案科目：初中数学 来源：素质教育新学案·初中几何·第三册 题型：044
解答题
如图所示，已知⊙O的内接正三角形ABC的边长为
，P为劣弧AC上的一动点，AP的延长线交BC的延长线于点D．
(1)求⊙O的半径R的长；
(2)设AP＝x，AD＝y，当点P在劣弧AC上运动时，求y与x之间的函数关系式；
(3)求当x为何值时PB＝PD．
查看答案和解析>>
科目：初中数学 来源：学习周报 数学 沪科九年级版 2009－2010学年 第18期 总第174期 沪科版 题型：013
正三角形的内切圆半径
r与外接圆半径R之间的关系为4R＝5r
3R＝4r
2R＝3r
R＝2r
查看答案和解析>>
科目：初中数学 来源：广东省汕头市金平区2011届九年级毕业模拟考试数学试题 题型：044
阅读材料并解答问题：
与正三角形各边都相切的圆叫做正三角形的内切圆，与正四边形各边都相切的圆叫做正四边形的内切圆，…，与正n边形各边都相切的圆叫做正n边形的内切圆，设正n(n≥3)边形的面积为S正n边形，其内切圆的半径为r，试探索正n边形的面积．(结果可用三角函数表示)
如图①，当n＝3时，设AB切圆O于点C，连结OC，OA，OB，
∴OC⊥AB，OA＝OB，∴∠AOC＝
AOB，AB＝2BC．
在Rt△AOC中，
，OC＝r，
∴AC＝r·tan60°，AB＝2r·tan60°，
∴S△OAB＝
·r·2rtan60°＝r2tan60°，
∴S正三角形＝3S△OAB＝3r2·tan60°．
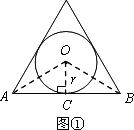
(1)如图②，当n＝4时，仿照(1)中的方法和过程可求得：S正四边形＝________；
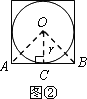
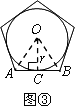
(2)如图③，当n＝5时，仿照(1)中的方法和过程求S正五边形；
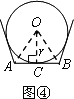
(3)如图④，根据以上探索过程，请直接写出S正n边形________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
．
________，边长
________，高h＝________．