
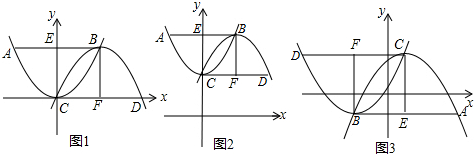
���� ��1��������AB��x�ᣬ��Ȼ��A��B����������y1=x2�ĶԳ���Գƣ��ɵ�AC=BC����֪AE=BE������������y2=a2x2+b2x+c2�Ե�BΪ�����ҹ���C���ֱ����B��C��x���ƽ���ߣ���֤���ı���ECFBΪ�����Σ�
����������y1�Ľ���ʽ�����A�����꣬�ٸ����ı���ECFBΪ�������г���A�ᡢ������Ĺ�ϵʽ���Դ�ȷ����A�����꣮
��2�������ı���ECFBΪ�����Σ��ɵ�CF=BF������C��0��1��������B��x��x+1����x��0���̶���ô𰸣�
�ڽ�y1�Ľ���ʽд�ɶ���ʽ������y1=-$\frac{1}{3}$��x-h��2+k�����ȸ��������ε��ص�������B�����꣬����B���������������y1�Ľ���ʽ�У��ɴ����m��ֵ��������y2�Ե�BΪ���㣬����д�ɶ���ʽ���ٽ���A���������������ȷ��a2��ֵ��
��3���ڣ�2���ٵĽ������У����Dz��ѿ���$\frac{1}{2}$CD=$\frac{1}{2}$AB=m=-|$\frac{1}{{a}_{1}}$|����$\frac{1}{2}$AB�ij������������������߶Գ���IJ�ľ���ֵ����ô������$\frac{1}{2}$CD�ij�����Ϊ������ϵ�г���ϵʽ���ݴ����b1��b2�Ĺ�ϵʽ��
��� �⣺��1����֤������AB��x�ᣬ
��A��B����y��Գƣ���AE=BE��
�֡�AE=BF��
��AB��x�ᣬ
���ECF=90�㣬
��BF��CD��
���CFB=��EBF=90�㣬
���ı���ECFBΪ���Σ�
�����ECFB������
�ڡ��ı���ECFBΪ�����Σ�
��CF=BF��
���B��x��x����x��0��
��x=x2��
��ã�x=1��
���B��1��1����
���A��-1��1����
��2���١��ı���ECFBΪ�����Σ�
��CF=BF��
��C��0��1����
��B��x��x+1����x��0��
��x+1=x2+1��
��ã�x=1��
���B��1��2����
��CF=1��
��CD=2��
����y1=-$\frac{1}{3}{x^2}+{b_1}x+{c_1}$=-$\frac{1}{3}$��x-h��2+k����C��h��k����B��h+m��k+m����
��B��y=-$\frac{1}{3}$��x-h��2+k�ϣ�
��k+m=-$\frac{1}{3}$��h+m-h��2+k��
��ã�m=-3��
��B��h-3��k-3����
��y2=a2x2+b2x+c2=a2��x-h+3��2+k-3��
����C��h��k����
��k=a2��h-h+3��2+k-3��
��ã�a2=$\frac{1}{3}$��
��3���ɣ�2����֪��a2=-a1��
�ɣ�2����֪��$\frac{1}{2}$AB=$\frac{1}{2}$CD=m=-|-$\frac{{b}_{1}}{{2a}_{1}}$-��-$\frac{{b}_{2}}{2{a}_{2}}$��|=-|$\frac{{b}_{1}+{b}_{2}}{2{a}_{1}}$|��
��m=-|$\frac{1}{{a}_{1}}$|[�ɣ�2����֪]��
��|$\frac{{b}_{1}+{b}_{2}}{2{a}_{1}}$|=|$\frac{1}{{a}_{1}}$|��
��ã�b1+b2=��2��
��b1=-b2+2��b1=-b2-2��
���� �������ڶ��κ������ۺ��⣬�����˶��κ����������Լ������ε��ж������ʣ�ע�����ն��κ����ĶԳ������������Ĺ�ϵ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ƽ��ֱ������ϵ�У�����OABC�ĶԽ���AC=12����ACO=30�㣬
��ͼ��ƽ��ֱ������ϵ�У�����OABC�ĶԽ���AC=12����ACO=30�㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
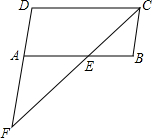 ��ͼ����֪?ABCD����E�ڱ�AB�ϣ�����CE���ӳ���DA���ӳ����ڵ�F����AE=AF����֤��AB=DF��
��ͼ����֪?ABCD����E�ڱ�AB�ϣ�����CE���ӳ���DA���ӳ����ڵ�F����AE=AF����֤��AB=DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ�κ���y=kx+b��ͼ��A��B���㣬��kx+b��0�Ľ⼯��x��-3��
��ͼ��ʾ��һ�κ���y=kx+b��ͼ��A��B���㣬��kx+b��0�Ľ⼯��x��-3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com