
分析 首先计算乘方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
解答 解:(2017-π)0+(-$\frac{1}{3}$)-1+|$\sqrt{3}$-1|-2sin60°
=1-3+$\sqrt{3}$-1-2×$\frac{\sqrt{3}}{2}$
=-$\sqrt{3}$
点评 此题主要考查了实数的运算,零指数幂、负整数指数幂以及特殊角的三角函数值的求法,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
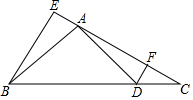 如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.
如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:| 组别 | 成绩(分) | 频数 |
| A | 50≤x<60 | 6 |
| B | 60≤x<70 | m |
| C | 70≤x<80 | 20 |
| D | 80≤x<90 | 36 |
| E | 90≤x<100 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com