
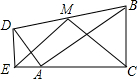
 (2012•拱墅区一模)把两个直角边长分别为3、4与9、12的Rt△ADE和Rt△ABC按照如图所示的位置放置,已知DE=4,AC=12,且E,A,C三点在同一直线上,连接BD,取BD的中点M,连接ME,MC,则△EMC与△DAB面积的比值为( )
(2012•拱墅区一模)把两个直角边长分别为3、4与9、12的Rt△ADE和Rt△ABC按照如图所示的位置放置,已知DE=4,AC=12,且E,A,C三点在同一直线上,连接BD,取BD的中点M,连接ME,MC,则△EMC与△DAB面积的比值为( )| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
| 1 |
| 2 |
| 13×15 |
| 4 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
| 13×15 |
| 4 |
| 13×15 |
| 4 |
| 1 |
| 2 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com