
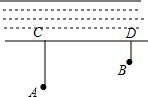
 如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.
如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少. 分析 作点B关于河岸的对称点B′,连接AB′交CD于点P,过点B′作B′E⊥AC,垂足为E,由轴对称的性质和两点之间线段最短可知AB′的长度即为最短路程.
解答 解:作点B关于河岸的对称点B′,连接AB′交CD于点P,过点B′作B′E⊥AC,垂足为E.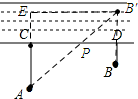
由轴对称的性质可知:PB=PB′,DB′=DB.
∴PA+PB=AP+PB′.
由两点之间线段最短可知;当点A、P、B′在一条直线上时,PA+PB最短.
在Rt△AEB′中,AB′=$\sqrt{A{E}^{2}+EB{′}^{2}}$=$\sqrt{60{0}^{2}+80{0}^{2}}$=1000.
点评 本题主要考查的是轴对称的性质、勾股定理的应用,明确当点A、P、B′在一条直线上时PA+PB最短是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 所有的有理数都能用数轴上的点来表示 | |
| B. | 有理数分为正数和负数 | |
| C. | 符号不同的两数互为相反数 | |
| D. | 两数相减,差一定小于被减数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com