
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | 0 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
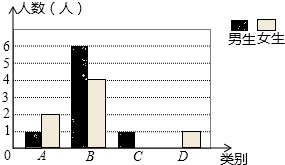 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 3 | 0.15 |
| B | 80≤x<90 | 10 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | d |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
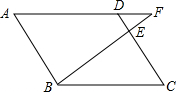 如图,在边长为4的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为$\frac{4}{3}$.
如图,在边长为4的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
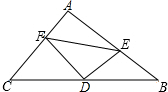 如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.
如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由$\frac{x}{3}-1=\frac{1-x}{2}$,得2x-1=3-3x | |
| B. | 由$\frac{x-2}{2}-\frac{3x-2}{4}=-1$,得2(x-2)-3x-2=-4 | |
| C. | 由$\frac{y+1}{2}=\frac{y}{3}-\frac{3y-1}{6}$-y,得3y+3=2y-3y+1-6y | |
| D. | 由$\frac{x}{4}$+1=$\frac{0.3x+1}{0.1}$+1.2,得$\frac{x}{4}$+1=$\frac{3x+10}{1}$+12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com