
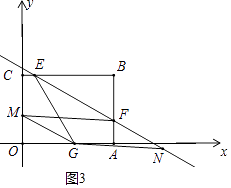
【题目】如图,四边形OABC为矩形,A点在x轴上,C点在y轴上,矩形一角经过翻折后,顶点B落在OA边的点G处,折痕为EF,F点的坐标是(4,1),∠FGA=30°.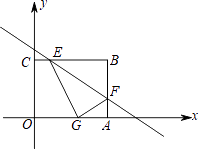
(1)求B点坐标.
(2)求直线EF解析式.
(3)若点M在y轴上,直线EF上是否存在点N,使以M、N、F、G为顶点的四边形是平行四边形?若存在,求N点的坐标;若不存在,请说明理由.
【答案】
(1)解:∵F点的坐标是(4,1),
∴FA=1,OA=4,
∵∠FGA=30°,
∴GA= ![]() ,FG=2,
,FG=2,
由折叠的性质知BF=FG=2,
∴AB=3,
∵四边形OABC为矩形,
∴CB=OA=4,
∴B点坐标为(4,3);
(2)解:∠AFG=90°﹣30°=60°,由折叠的性质知∠EFB=∠EFG= ![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴BE= ![]() BF=2
BF=2 ![]() ,
,
∴CE=4﹣2 ![]() ,
,
∴E(4﹣2 ![]() ,4),
,4),
设直线EF的解析式是y=kx+b,
∴ ![]() ,
,
解得 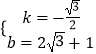 ,
,
∴直线EF的解析式是y=﹣ ![]() x+2
x+2 ![]() +1
+1
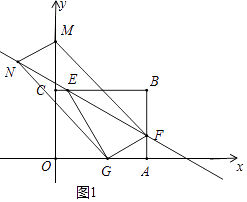
(3)解:①如图1中,当四边形MNGF是平行四边形时,易知点N的横坐标为﹣ ![]() ,
,
∵点N在直线EF上,
∴N(﹣ ![]() ,2
,2 ![]() +
+ ![]() ).
).
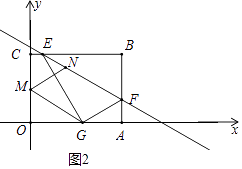
②如图2中,当四边形MNFG是平行四边形时,易知点N的横坐标为 ![]() ,
,
∵点N在直线EF上,
∴N( ![]() ,2
,2 ![]() ﹣
﹣ ![]() ).
).
③如图3中,当四边形MFNG是平行四边形时,易知点M坐标为(0, ![]() )
)
∵FG与MN相互垂直平分,
∴N(8﹣ ![]() ,2﹣
,2﹣ ![]() ).
).
【解析】(1)利用翻折不变性即可解决问题;(2)求出E、F两点坐标,利用待定系数法即可解决问题;(3)分三种情形①如图1中,当四边形MNGF是平行四边形时,易知点N的横坐标为﹣ ![]() ,由此即可解决问题;②如图2中,当四边形MNFG是平行四边形时,易知点N的横坐标为
,由此即可解决问题;②如图2中,当四边形MNFG是平行四边形时,易知点N的横坐标为 ![]() ,由此即可解决问题;③如图3中,当四边形MFNG是平行四边形时,易知点M坐标为(0,
,由此即可解决问题;③如图3中,当四边形MFNG是平行四边形时,易知点M坐标为(0, ![]() ),根据FG与MN相互垂直平分,利用中点坐标公式,计算即可;
),根据FG与MN相互垂直平分,利用中点坐标公式,计算即可;
【考点精析】通过灵活运用确定一次函数的表达式和勾股定理的概念,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


科目:初中数学 来源: 题型:
【题目】某自治州自然风景优美,每天吸引大量游客前来游览,经统计,某段时间内来该州风景区游览的人数约为36000人,用科学记数法表示36000为( )
A.36×103
B.0.36×106
C.0.36×104
D.3.6×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘,由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠A=30°,过点B、C的⊙O交AB于D,交AC于E,点F在AE上,连接DE、DC、BE和DF,已知BC=EC,AD=AF.
(1)求证:DF是⊙O的切线;
(2)当BC=4时,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·江西吉安模拟)如图,是一个正六边形转盘被分成6个全等的正三角形,指针位置固定.转动转盘后任其自由停止,其中的某个三角形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个三角形的公共边时,当作指向右边的三角形),这时称转动了转盘1次.
(1)下列说法不正确的是 .
A.出现1的概率等于出现3的概率
B.转动转盘30次,6一定会出现5次
C.转动转盘3次,出现的3个数之和等于19,这是一个不可能发生的事件
(2)当转动转盘36次时,出现2这个数大约有多少次?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com