
【题目】如图,下列说法错误的是( ).
①∠1和∠3是同位角;②∠1和∠5是同位角;③∠1和∠2是同旁内角;④∠1和∠4是内错角.
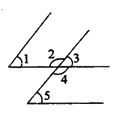
A. ①② B. ②③ C. ②④ D. ③④
【答案】C
【解析】
根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,分别进行分析可得答案.
①∠1与∠3是同位角,原题说法正确;
②∠1与∠5不是同位角,故原题说法错误;
③∠1与∠2是同旁内角,原题说法正确;
④∠1与∠4不是内错角,原题说法错误;
故选C.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,平行四边形纸片ABCD中,AD=5,S甲行四边形纸片ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
求证:四边形AFF′D是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)求证:四边形AECF是菱形;
(2)若AC=4,BE=1,直接写出菱形AECF的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,当直线BC、DC被直线AB所截时,∠1的同位角是_______,同旁内角是_______;当直线AB、AC被直线BC所截时,∠1的同位角是________;当直线AB、BC被直线CD所截时,∠2的内错角是________
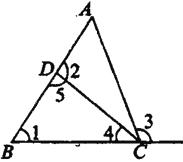
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务。
阿基米德(Archimedes,公元前287~公元前212年,古希腊)是有史以来最伟大的数学家之一.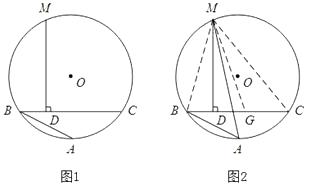
阿基米德折弦定理:如图1,AB和BC是圆O的两条弦(即折线ABC是圆的一条折弦), BC>AB,M是 ![]() 的中点,即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
的中点,即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
证明:如图2,在CB上截取CG=AB,连接MA、MB、MC、MG。因为M是弧ABC的中点,所以MA=MC.
任务:
(1)请按照上面的证明思路,完整证明阿基米德折弦定理,即CD=AB+BD。
(2)如图3,已知等边△ABC内接于圆O,AB=1,D为 ![]() 上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.
上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一慢车和一快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,试根据图象回答下列问题:

(1)由图象你可以得到哪些信息?
(2)求慢车、快车的速度.
(3)求A,B两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C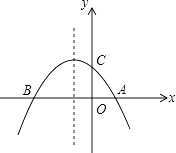
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com