
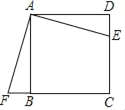
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF.
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
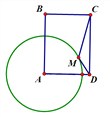
【题目】如图,已知矩形ABCD,AB=8,BC=6,以点A为圆心,5为半径作圆,点M为圆A上一动点,连接CM,DM,则![]() CM+MD的最小值为_________.
CM+MD的最小值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设实数a,b,c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x-a|+|x+b|+|x-c|的最小值为( )
A. ![]() B. |b| C. a+b D. -c-a
B. |b| C. a+b D. -c-a
查看答案和解析>>
科目:初中数学 来源: 题型:
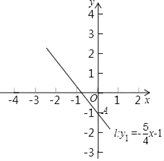
【题目】如图,直线l:y1=﹣![]() x﹣1与y轴交于点A,一次函数y2=
x﹣1与y轴交于点A,一次函数y2=![]() x+3图象与y轴交于点B,与直线l交于点C.
x+3图象与y轴交于点B,与直线l交于点C.
(1)画出一次函数y2=![]() x+3的图象;
x+3的图象;
(2)求点C坐标;
(3)如果y1>y2,那么x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
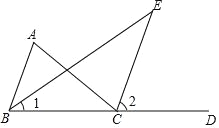
【题目】如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E,以下是小明的证明过程,请在括号里填写理由.
证明:∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知)
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(_________)
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质)
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知)
∴∠ACD=2∠2,∠ABC=2∠1(_______)
∴∠A=2∠2﹣2∠1(_________)
=2(∠2﹣∠1)(_________)
=2∠E(等量代换)
(2)如果∠A=∠ABC,求证:CE∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的好点,但点D是【B,A】的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

(1)数______所表示的点是【M,N】的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
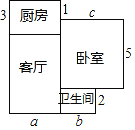
【题目】小王家新买的一套住房的建筑平面图如图所示(单位:米).
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=9,b=4,c=7,试求出小王家这套住房的具体面积.
(3)地面装修要铺设瓷砖,公司报价是:客厅地面每平方米200元,卧室地面每平方米150元,厨房地面每平方米120元,卫生间地面每平方米100元.在(2)的条件下,小王一共要花多少钱?
(4)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小宇家购买这套住房时向银行申请贷款的金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
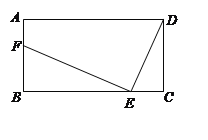
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若![]() ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com