
分析 (1)按要求分别进行计算,得到商都是-$\frac{1}{2x}$;
(2)先看分式的符号,第一个+,第二个-,依次可以看作(-1)n+1,分母的系数是1、2、4、8、都是2的幂;分母中x项,依次为x、x2、x3、x4…,得出第n个分式.
解答 解:(1)-$\frac{1}{2x2}÷\frac{1}{x}$=-$\frac{1}{2x}$,$\frac{1}{4{x}^{3}}$÷(-$\frac{1}{2{x}^{2}}$)=-$\frac{1}{2x}$,-$\frac{1}{8{x}^{4}}$÷$\frac{1}{4{x}^{3}}$=-$\frac{1}{2x}$,…,
发现:一个分式与它前一个分式的商,都是-$\frac{1}{2x}$;
(2)第1个分式:$\frac{1}{x}$,
第2个分式:-$\frac{1}{2{x}^{2}}$,
第3个分式:$\frac{1}{4{x}^{3}}$,
第4个分式:-$\frac{1}{8{x}^{4}}$,
…
第n个分式:$\frac{(-1)^{n+1}}{{2}^{n-1}{x}^{n}}$.
点评 本题考查了分式的定义、分式的除法和数字类的规律问题,分式的除法运算,根据除以一个数等于乘以这个数的倒数进行计算,对于分式中的规律问题,分解为三个问题考虑:分式的符号、分子、分母;把各个规律结合在一起,得出结论即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
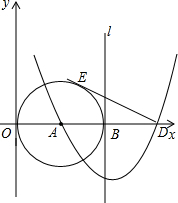 如图,已知点A(4,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
如图,已知点A(4,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
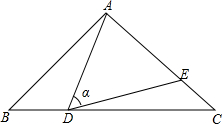 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=α,DE交AC于点E.下列结论:
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=α,DE交AC于点E.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
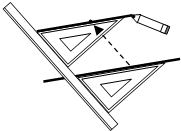 如图,图中给出了过直线外一点作已知直线的平行线的方法,其依据的是( )
如图,图中给出了过直线外一点作已知直线的平行线的方法,其依据的是( )| A. | 同位角相等,两直线平行 | B. | 同旁内角互补,两直线平行 | ||
| C. | 内错角相等,两直线平行 | D. | 同平行于一条直线的两直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com