
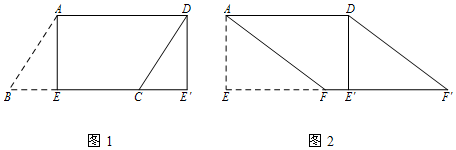
分析 (1)根据矩形的判定方法即可判定;
(2)①通过计算证明AF=AD=5,证明四边形AFF′D是平行四边形即可;
②连接AF',DF,分别利用勾股定理计算即可;
解答 (1)解:如图1中,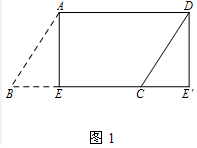
∵四边形ABCD是平行四边形,
∴AD=BC,
∵BE=CE′,
∴AD∥EE′,AD=EE′,
∴四边形AEE′D是平行四边形,
∵∠AEE′=90°,
∴四边形AEE′D是矩形,
故选C.
(2)如图2中,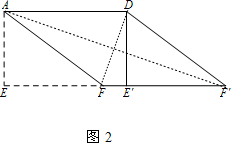
①证明:∵AD=5,S□ABCD=15,
∴AE=3.
又∵在图2中,EF=4,
∴在Rt△AEF中,AF═5.
∴AF=AD=5,
又∵AF∥DF',AF=DF,
∴四边形AFF'D是平行四边形.
∴四边形AFF'D是菱形.
②解:连接AF',DF,
在Rt△DE'F中,∵E'F=E'E-EF=5-4=1,DE'=3,
∴DF═$\sqrt{E′{D}^{2}+E′{F}^{2}}$=$\sqrt{10}$.
在Rt△AEF'中,∵EF'=E'E+E'F'=5+4=9,AE=3,
∴AF'═$\sqrt{A{E}^{2}+EF{′}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$.
点评 本题考查四边形综合题、矩形的判定、菱形的判定、勾股定理等知识,解题的关键是熟练掌握矩形、菱形的判定方法,属于中考常考题型.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
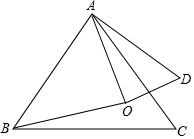 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | α=135°+$\frac{β+γ}{2}$ | B. | γ>β+45° | ||
| C. | ∠β与∠γ有可能互补 | D. | α+β+γ<270° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
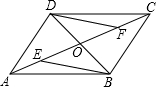 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
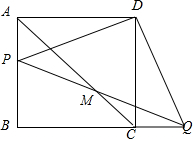 如图,在正方形ABCD中,AB=2,点P为边AB上一点.将△ADP旋转到△CDQ的位置上.连接AC,PQ交于点M,则$\sqrt{2}$AM-AP的值为2.
如图,在正方形ABCD中,AB=2,点P为边AB上一点.将△ADP旋转到△CDQ的位置上.连接AC,PQ交于点M,则$\sqrt{2}$AM-AP的值为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com