
【题目】如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值_____

【答案】2![]() +4.
+4.
【解析】
由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论.
∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形,
由旋转的性质得,BE=AD,
∴C△DBE=BE+DB+DE=AB+DE=4+DE,
∵△CDE是等边三角形,
∴DE=CD,
∴C△DBE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,CD=2![]() ,
,
∴△BDE的最小周长=CD+4=2![]() +4,
+4,
故答案为:2![]() +4.
+4.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
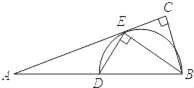
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
(1)判断直线AC与△DBE外接圆的位置关系,并说明理由;
(2)若AD=6,AE=6![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实素质教育要求,促进学生全面发展,我市某中学2014年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2016年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2014年到2016年,该中学三年为新增电脑共投资多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,6),点B(4,3),P是x轴上的一个动点.作OQ⊥AP,垂足为点Q,连接QB,则△AQB的面积的最大值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x–2)(x–3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是
A. 当m=0时,x1=2,x2=3
B. m>–![]()
C. 当m>0时,2<x1<x2<3
D. 二次函数y=(x–x1)(x–x2)+m的图象与x轴交点的坐标为(2,0)和(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数( )
①近似数![]() 精确到十分位:
精确到十分位:
②在![]() ,
,![]() ,
,![]() ,
,![]() 中,最小的数是
中,最小的数是![]()
③如图①所示,在数轴上点![]() 所表示的数为
所表示的数为![]()
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”
⑤如图②,在![]() 内一点
内一点![]() 到这三条边的距离相等,则点
到这三条边的距离相等,则点![]() 是三个角平分线的交点
是三个角平分线的交点
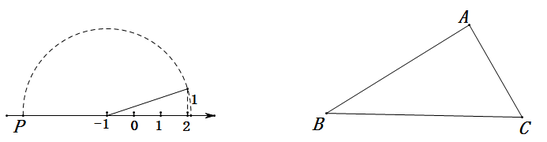
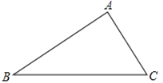
图① 图②
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在越来越多的人在用微信付款、转账,也可以提现.把微信账户里的钱转到银行卡里叫做提现.从2016年3月1日起,每个微信账户终身享有![]() 元免费提现额度,当累计提现额度超过
元免费提现额度,当累计提现额度超过![]() 元时,超出
元时,超出![]() 元的部分要支付
元的部分要支付![]() 的手续费.以后每次提现都要支付所提现金额的
的手续费.以后每次提现都要支付所提现金额的![]() 的手续费.
的手续费.
(1)张老师在今年第一次进行了提现,金额为![]() 元,他需要支付手续费 元.
元,他需要支付手续费 元.
(2)李老师从2016年3月1日起至今,用自己的微信账户共提现![]() 次,
次, ![]() 次提现的金额和手续费如下表:
次提现的金额和手续费如下表:
第一次提现 | 第二次提现 | 第三次提现 | |
提现金额(元) |
|
|
|
手续费(元) |
|
|
|
请问李老师前![]() 次提现的金额分别是多少元?
次提现的金额分别是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com