
【题目】已知数轴上有A、B、C三个点,分别表示有理数-12、-5、5,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为 t秒。

(1)用含t的代数式表示P到点A和点C的距离:PA=________ , PC=________。
(2)当点P从点A出发,向点C移动,点Q以每秒3个单位从点C出发,向终点A移动,请求出经过几秒点P与点Q两点相遇?
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A,在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由。
【答案】(1))t;27-t;(2)经过4.25秒点P与点Q两点相遇;(3)点P表示的数为-![]() , -
, -![]() ,
, ![]() ,
, ![]() .
.
【解析】
(1)根据P点位置进而得出PA,PC的距离;
(2)根据两点运动路程之和等于线段AC的长即可得到方程求解;
(3)分别根据P点与Q点相遇前以及相遇后进而分别分析得出即可.
(1)t;27-t
(2)依题可得:
PA=t,CQ=3t,
∵P、Q两点相遇,
∴t+3t=5-(-12),
解得:t= ![]() =4.25,
=4.25,
答:经过4.25秒点P与点Q两点相遇.
(3)依题可得:
AP=t,AC=5+12=17,
∵动点P的速度是每秒1个单位,
∴点P运动到B点时间为:(-5+12)÷1=7(秒),
①当点P在点Q右侧,且Q点还没有追上P点时(如图1),
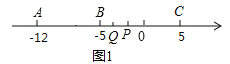
∵动点Q的速度是每秒3个单位,
∴AQ=3(t-7),
∵P、Q两点之间的距离为2个单位,
∴AP=AQ+PQ,
即3(t-7)+2=t,
解得:t=;
∴OP=OA-AP=12-![]() =
=![]() ,
,
∴点P表示的数为:-![]() ;
;
②当点P在点Q左侧,且Q点追上了P点时(如图2),
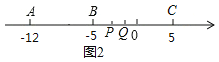
∵动点Q的速度是每秒3个单位,
∴AQ=3(t-7),
∵P、Q两点之间的距离为2个单位,
∴AQ=AP+PQ,
即3(t-7)=2+t,
解得:t=![]() ;
;
∴OP=OA-AP=12-![]() =
=![]() ,
,
∴点P表示的数为:-![]() .
.
③当点Q到达C点后,且P点在Q点左侧时(如图3),
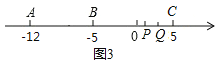
∵动点Q的速度是每秒3个单位,
∴AC+CQ=3(t-7),
∵AC=17,
∴CQ=3(t-7)-17,
∵P、Q两点之间的距离为2个单位,
∴AP+PQ+CQ=AC,
即t+2+3(t-7)-17=17,
解得:t=![]() ;
;
∴OP=AP-OA=![]() -12=
-12=![]() ,
,
∴点P表示的数为:![]() ;
;
④当点Q到达C点后,且P点在Q点右侧时(如图4),
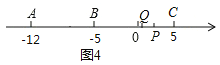
∵AP=t,PQ=2,
∴AQ=AP-PQ=t-2,
∵动点Q的速度是每秒3个单位,
∴AC+CQ=3(t-7),
∵AC=17,
∴CQ=3(t-7)-17,
∵P、Q两点之间的距离为2个单位,
∴AQ+CQ=AC,
即t-2+3(t-7)-17=17,
解得:t=![]() ;
;
∴OP=AP-OA=![]() -12=
-12=![]() ,
,
∴点P表示的数为:![]() .
.
综上所述:点P表示的数为-![]() ,-
,-![]() ,
,![]() ,
,![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(3+![]() )(3﹣
)(3﹣![]() )﹣(1﹣
)﹣(1﹣![]() )2
)2
(3)我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选一个,并选择你认为适当的方法解这个方程.
①x2﹣4x﹣1=0 ②x(2x+1)=8x﹣3 ③x2+3x+1=0 ④x2﹣9=4(x﹣3)
我选择第几个方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE. 
(1)求证:AF=DE;
(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了 28m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为m立方米,当 m>20时,则该用户应缴纳的的水费为________元(用含 a、m的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水 40m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,试求甲、乙两用户一个月共缴纳的水费(用含 x的整式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠BAC=90°,AC=AB,以AB为斜边在△ABC内部作Rt△ABD,连接CD,若∠ADC=135°,S△ABD=9,则线段AD的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,组合烟花的高为h,则组合烟花侧面包装纸的面积至少需要(接缝面积不计)( ) 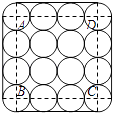
A.26πrh
B.24rh+πrh
C.12rh+2πrh
D.24rh+2πrh
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com