
分析 首先解不等式组,根据不等式组只有三个正整数解,即可确定a的范围.
解答 解:$\left\{\begin{array}{l}{2x-3≥1①}\\{\frac{2x-5a}{3}-x>2②}\end{array}\right.$
解不等式①得,x≥2,
解不等式②得,x<-5a-6.
则不等式组的解集是:2≤x<-5a-6,
则正整数解是2,3,4;
则4<-5a-6≤5,
解得-$\frac{11}{5}$≤a<-2.
故答案是:-$\frac{11}{5}$≤a<-2.
点评 本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | k1<0,k2>0 | B. | k1>0,k2<0 | C. | k1、k2同号 | D. | k1、k2异号 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
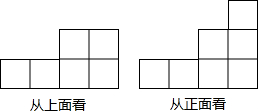 由一些大小相同的小正方体组成的简单几何体从正面和上面看到的平面图形如图所示.
由一些大小相同的小正方体组成的简单几何体从正面和上面看到的平面图形如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com