
【题目】如图,边长为2的正方形ABCD,点P在边BC上(不与B,C重合),将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.
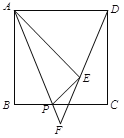
(1)如图,若∠BAP=30°,求∠AFE的度数;
(2)若点E恰为线段DF的中点时,请通过运算说明点P会在线段BC的什么位置?直接写出此时
∠AFD的度数;
(3)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论.
【答案】(1)45°;(2)点P在线段BE的垂直平分线上,45°;
(3)∠AFD的度数不会发生变化,理由见解析
【解析】分析:(1)当点P在线段BC上时,由折叠得到一对角相等,再利用正方形性质求出∠DAE度数,在三角形AFD中,利用内角和定理求出所求角度数即可;(2)由E为DF相等,得到P为BC中点,如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,得到AF垂直平分BE,进而得到三角形BOP与三角形EOG全等,利用全等三角形对应边相等得到BP=EG=1,得到P为BC中点,进而求出所求角度数即可;(3)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数不会发生变化,理由为:作AG⊥DF于点G,如图1(a)所示,利用折叠的性质及三线合一性质,根据等式的性质求出∠1+∠2的度数,即为∠FAG度数,即可求出∠F度数;
本题解析:
(1)∵∠EAP=∠BAP=30°,
∴![]() ,
,
在△ADE中,AD=AE,∠DAE=30°,
∴![]() ,
,
在△AFD中,∠FAD=30°+30°=60°,∠ADF=75°,
∴![]() ;
;
(2)点E为DF的中点时,P也为BC的中点,理由如下:
如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,
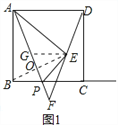
∵EG∥AD,DE=EF,
∴![]() ,
,
∵AB=AE,
∴点A在线段BE的垂直平分线上,
同理可得点P在线段BE的垂直平分线上,
∴AF垂直平分线段BE,
∴OB=OE,
∵GE∥BP,
∴∠OBP=∠OEG,∠OPB=∠OGE,
∴△BOP≌△EOG,
∴BP=EG=1,即P为BC的中点,
![]() 的度数为
的度数为![]() ;
;
(3)∠AFD的度数不会发生变化,
证明:作AG⊥DF于点G,如图2所示,
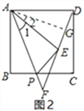
在△ADE中,AD=AE,AG⊥DE,
∵AG平分∠DAE,即∠2=∠DAG,且∠1=∠BAP,
∴![]() ,即∠FAG=45°,
,即∠FAG=45°,
则![]() .
.


科目:初中数学 来源: 题型:
【题目】将二次函数y=x2+4x+3化成顶点式,变形正确的是( )
A. y=(x﹣2)2﹣1 B. y=(x+1)(x+3)
C. y=(x﹣2)2+1 D. y=(x+2)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)物体向右运动4m记作+4m,那么物体向左运动3m,应记作____m.
(2)单项式﹣![]() 的系数是____.
的系数是____.
(3)一个数的倒数是﹣1,这个数是____.
(4)|a|=5,|b|=3,且|a+b|=a+b,则ab=____.
(5)按下列程序输入一个数x,若输入的数x=0,则输出结果为____.
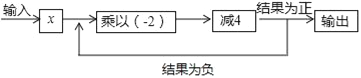
(6)如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“![]() ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为__________________.
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为__________________. 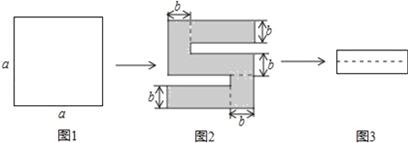
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于角的说法正确的是( )
A. 两条射线组成的图形叫做角 B. 角的大小与这个角的两边的长短无关
C. 延长一个角的两边 D. 角的两边是射线,所以角不可度量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120)。已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1) 当速度为50km/h、100km/h时,该汽车的耗油量分别为_____L/km、____L/km.
(2) 求线段AB所表示的y与x之间的函数表达式
(3) 速度是多少时,该汽车的耗油量最低?最低是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )

A.②④⑤⑥ B.①③⑤⑥ C.②③④⑥ D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5颗粒为小于或等于0.0000025米的微粒,直径虽小,但活性强,易附带有毒、有害物质,且在大气中的停留时间长、输送距离远,因而对人体健康和大气环境质量的影响更大.0.0000025这个数字用科学记数法表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com