
分析 先估算出$\sqrt{2}$与$\sqrt{5}$的值,再利用逼近法估算出$\sqrt{26}$的取值范围,进而可得出结论.
解答 解:∵$\sqrt{2}$≈1.4,$\sqrt{5}$≈2.2,
∴5-$\sqrt{2}$≈3.6,2+$\sqrt{2}$≈3.4,2+$\frac{\sqrt{5}}{2}$≈3.1.
∵25<26<36,
∴5<$\sqrt{26}$<6,
∴$\sqrt{5}$<2+$\frac{\sqrt{5}}{2}$<2+$\sqrt{2}$<5-$\sqrt{2}$<$\sqrt{26}$.
点评 本题考查的是实数的大小比较,熟记$\sqrt{2}$与$\sqrt{5}$的近似值是解答此题的关键.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 基本事实和定理都是真命题 | |
| B. | 基本事实就是定理,定理就是基本事实 | |
| C. | 基本事实和定理都可以作为推理论证的依据 | |
| D. | 基本事实的正确性不需证明,定理的正确性需证明 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
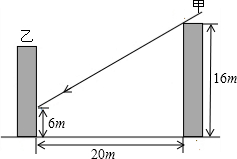 如图,某小区宿舍楼甲楼坐落在正南正北方向,高16m,现在在甲楼后盖座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼6m,若甲楼的影子刚好不影响乙楼的采光,两楼距离应是多少m?
如图,某小区宿舍楼甲楼坐落在正南正北方向,高16m,现在在甲楼后盖座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼6m,若甲楼的影子刚好不影响乙楼的采光,两楼距离应是多少m?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com