
 如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )
如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )| A. |  | B. |  | C. |  | D. |  |
科目:初中数学 来源: 题型:解答题
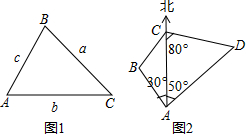 【阅读新知】
【阅读新知】查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )| A. | 95° | B. | 90° | C. | 85° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
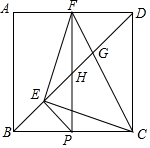 如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.
如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)
在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
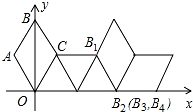 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )| A. | (1345,0) | B. | (1345,$\frac{\sqrt{3}}{2}$) | C. | (1345.5,0) | D. | (1345.5,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.
如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com