
【题目】阅读下列材料,然后解答后面的问题.
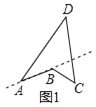
(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(2)性质探究:请完成凹四边形一个性质的证明.
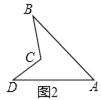
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
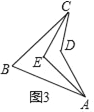
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B=_____°.
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)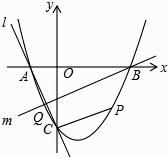
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用白铁皮做罐头盒,每张铁皮可做盒身25个,或做盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?
①设用x张制盒身,可得方程2×25x=40(36﹣x);
②设用x张制盒身,可得方程25x=2×40(36﹣x);
③设用x张制盒身,y张制盒底,可得方程组![]() ;
;
④设用x张制盒身,y张制盒底,可得方程组![]() ;其中正确的是( )
;其中正确的是( )
A. ①④ B. ②③ C. ②④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y= ![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )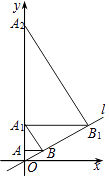
A.(0,42015)
B.(0,42014)
C.(0,32015)
D.(0,32014)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车以汽车站为出发点,在东西方向的城市道路上进行营运,若规定向东为正,向西为负,行车依先后顺序记录如下(单位:千米):
+4,-5,+9,-3,+6,-3,-8,-4,+7,-6.
(1)计算说明出租车将最后一名乘客送到目的地,此时离汽车站多远?在汽车站什么方向?
(2)若该出租车每千米收费标准为3元,求出租车的营业额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块矩形场地,场地的长是宽的2倍.计划在矩形场地上修建宽都为2米的两条互相垂直的小路,如图,余下的四块小矩形场地建成草坪.四块小矩形草坪的面积之和为364平方米,求这个矩形场地的长和宽各是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在等腰梯形ABCD中,AD//BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD. 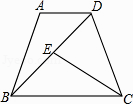
(1)证明:△ADB≌△EBC;
(2)直接写出图中所有的等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com