
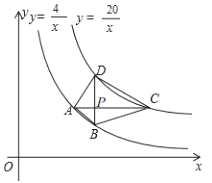
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() 的图象上,对角线
的图象上,对角线![]() 轴,且
轴,且![]() 于点P.已知点B的横坐标为4.
于点P.已知点B的横坐标为4.
(1)若点P的纵坐标为2,求直线AB的函数表达式.
(2)若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
科目:初中数学 来源: 题型:
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学校随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间![]() 分钟的学生记为
分钟的学生记为![]() 类,20分钟
类,20分钟![]() 分钟记为
分钟记为![]() 类,40分钟
类,40分钟![]() 分钟记为
分钟记为![]() 类,
类,![]() 分钟记为
分钟记为![]() 类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
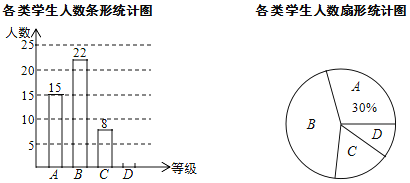
(1)这次共抽取了__________名学生进行调查统计,扇形统计图中![]() 类所对应的扇形圆心角大小为___________;
类所对应的扇形圆心角大小为___________;
(2)将条形统计图补充完整;
(3)如果该校共有2000名学生,请你估计该校![]() 类学生约有多少人?
类学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
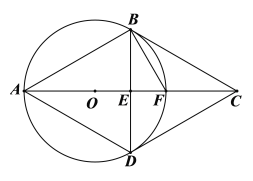
【题目】如图,菱形ABCD对角线交于点E,△ABD的外接圆⊙O交AC于点F.若FB=FC.
(1)证明:![]() =FEFA;
=FEFA;
(2)证明:BC是⊙O的切线;
(3)若EF=2,求出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
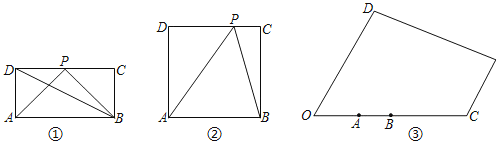
【题目】问题探究,
(1)如图①,在矩形ABCD中,AB=2AD,P为CD边上的中点,试比较∠APB和∠ADB的大小关系,并说明理由;
(2)如图②,在正方形ABCD中,P为CD上任意一点,试问当P点位于何处时∠APB最大?并说明理由;
问题解决
(3)某儿童游乐场的平面图如图③所示,场所工作人员想在OD边上点P处安装监控装置,用来监控OC边上的AB段,为了让监控效果最佳,必须要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 过点
过点![]() .
.
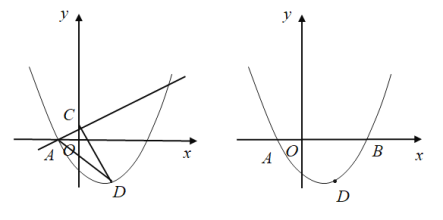
(1)求出抛物线解析式的一般式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做神奇四边形.顺次连接四边形各边中点得到的四边形叫做中点四边形.
(1)判断:
①在平行四边形、矩形、菱形中,一定是神奇四边形的是 ;
②命题:如图1,在四边形![]() 中,
中,![]() 则四边形
则四边形![]() 是神奇四边形.此命题是_____(填“真”或“假”)命题;
是神奇四边形.此命题是_____(填“真”或“假”)命题;
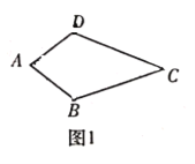
③神奇四边形的中点四边形是
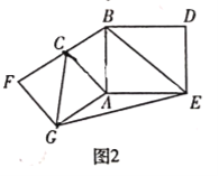
(2)如图2,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]()
①求证:四边形![]() 是神奇四边形;
是神奇四边形;
②若![]() ,求
,求![]() 的长;
的长;
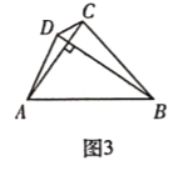
(3)如图3,四边形![]() 是神奇四边形,若
是神奇四边形,若![]() 分别是方程
分别是方程![]() 的两根,求
的两根,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙人文教用品商店欲购进![]() 、
、![]() 两种笔记本,用160元购进的
两种笔记本,用160元购进的![]() 种笔记本与用240元购进的
种笔记本与用240元购进的![]() 种笔记本数量相同,每本
种笔记本数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵10元.
种笔记本的进价贵10元.
(1)求![]() 、
、![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店准备购进![]() 、
、![]() 两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进
两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进![]() 种笔记本多少本?
种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与直线
与直线![]() 都经过
都经过![]() ,
,![]() 两点,该抛物线的顶点为
两点,该抛物线的顶点为![]() .
.
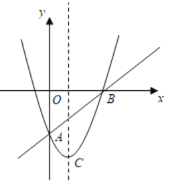
(1)求抛物线和直线![]() 的解析式;
的解析式;
(2)设点![]() 是直线
是直线![]() 下方抛物线上的一动点,求
下方抛物线上的一动点,求![]() 面积的最大值,并求
面积的最大值,并求![]() 面积最大时,点
面积最大时,点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com