
【题目】如图,已知线段![]() ,点
,点![]() 为线段外一点,且
为线段外一点,且![]() .
.
(1)请用直尺(不带刻度)和圆规在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() 的周长为
的周长为![]() (作图不必写作法,但要保留作图痕迹);
(作图不必写作法,但要保留作图痕迹);
(2)在(1)的条件下,若![]() ,
,![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的面积.
的面积.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
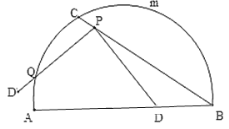
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.50 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
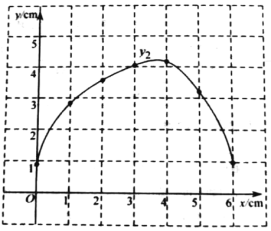
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
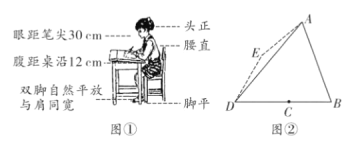
【题目】良好的坐姿习惯有利于青少年骨骼生长,有利于身体健康,那么首先要有正确的写字坐姿,身体上半部坐直,头部端正、目视前方,两手放在桌面上,两腿平放,胸膛挺起,理想状态下,如图①,将图①中的眼睛记为点![]() ,腹部记为点
,腹部记为点![]() ,笔尖记为点
,笔尖记为点![]() ,且
,且![]() 与桌面沿的交点记为点
与桌面沿的交点记为点![]() ,已知
,已知![]() ,点
,点![]() 到
到![]() 的距离为23cm,
的距离为23cm, ![]() .
.
(1)求![]() 的度数
的度数
(2)老师发现小亮同学写字姿势不正确,眼睛倾斜到图2的点![]() ,点
,点![]() 恰好在
恰好在![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,于是要求其纠正为正确的姿势,求眼睛所在的位置上升的距离(结果精确到1cm)
,于是要求其纠正为正确的姿势,求眼睛所在的位置上升的距离(结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
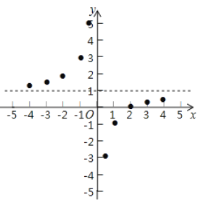
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,E为AB上一点,以AE为直径作⊙O与BC相切于点D,连接ED并延长交AC的延长线于点F.
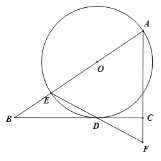
(1)求证:AE=AF;
(2)若BC=4,AC=3,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
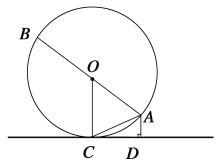
求证:(1)∠AOC=2∠ACD;(2)AC2=AB·AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若边长为6的正方形ABCD绕点A顺时针旋转,得正方形AB′C′D′,记旋转角为a.
(I)如图1,当a=60°时,求点C经过的弧![]() 的长度和线段AC扫过的扇形面积;
的长度和线段AC扫过的扇形面积;
(Ⅱ)如图2,当a=45°时,BC与D′C′的交点为E,求线段D′E的长度;
(Ⅲ)如图3,在旋转过程中,若F为线段CB′的中点,求线段DF长度的取值范围.
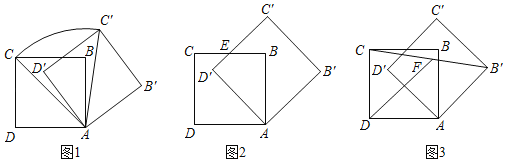
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com