
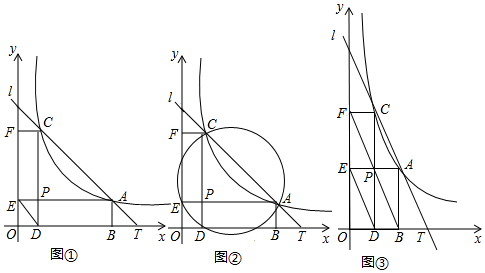
分析 (1)由P、E、D的坐标可表示出PA、EP、PC和DP的长,可证明△EPD∽△CPA,利用相似三角形的性质可证得结论;
(2)连接AD、EC,可证明△AEC≌△CDA,可得CD=AE,把A、C坐标代入直线l解析式,可求得k的值;
(3)假设在线段AT上存在点M,使得OM⊥AM,连接OM、OA,可表示出C、F、P、B的坐标,利用直线BF的解析式可求得a的值,可求得A点坐标,可求得T点坐标,在△OAT中,利用等积法可求得OM的长,在RtOMT中可求得MT的长,作MN⊥x轴,同理可求得MN的长,则可求得ON的长,可判断N在线段BT上,满足条件,从而可知存在满足条件的M点.
解答 (1)证明:
由题意可知P(c,$\frac{4}{c}$),E(0,$\frac{4}{a}$),D(c,0),
∴PA=a-c,EP=c,PC=$\frac{4}{c}$-$\frac{4}{a}$=$\frac{4(a-c)}{ac}$,DP=$\frac{4}{a}$,
∴$\frac{EP}{PA}$=$\frac{c}{a-c}$=$\frac{DP}{PC}$,且∠EPD=∠APC,
∴△EPD∽△CPA,
∴∠EDP=∠ACP;
(2)解:如图1,连接AD、EC,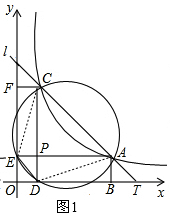
由(1)可知DE∥AC,
∴∠DEC+∠ECA=180°,
∵A、D、E、C四点在同圆周上,
∴∠DEC+∠DAC=180°,
∴∠ECA=∠DAC,
在△AEC和△CDA中
$\left\{\begin{array}{l}{∠ECA=∠DAC}\\{∠AEC=∠CDA}\\{AC=CA}\end{array}\right.$
∴△AEC≌△CDA(AAS),
∴CD=AE,即a=$\frac{4}{c}$,可得ac=4,
∵A、C在直线l上,
∴$\left\{\begin{array}{l}{ka+b=\frac{4}{a}}\\{kc+b=\frac{4}{c}}\end{array}\right.$,解得k=$\frac{\frac{4}{a}-\frac{4}{c}}{a-c}$=-$\frac{4}{ac}$=-1;
(3)假设在线段AT上存在点M,使OM⊥AM,连接OM、OA,作MN⊥x轴于点N,如图2,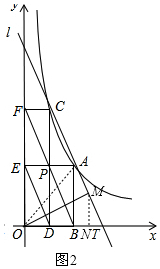
∵c=1,
∴C(1,4),F(0,4),P(1,$\frac{4}{a}$),B(a,0),
设直线BF的解析式为y=k′x+4,由题意可得$\left\{\begin{array}{l}{k′a+4=0}\\{k′+4=\frac{4}{a}}\end{array}\right.$,解得a=2,
∴A(2,2),
∴AP为△DCT的中位线,
∴T(3,0),
∴AT=$\sqrt{(3-1)^{2}+(0-2)^{2}}$=$\sqrt{5}$
∵S△OAT=$\frac{1}{2}$OT•AB=$\frac{1}{2}$AT•OM,
∴OM=$\frac{OT•AB}{AT}$=$\frac{3×2}{\sqrt{5}}$=$\frac{6}{\sqrt{5}}$,
在Rt△OMT中,MT=$\sqrt{O{T}^{2}-O{M}^{2}}$=$\sqrt{{3}^{2}-\frac{36}{5}}$=$\frac{3}{\sqrt{5}}$,
同理可求得MN=$\frac{OM•MT}{OT}$=$\frac{6}{5}$,
在Rt△OMN中,ON=$\sqrt{O{M}^{2}-M{N}^{2}}$=$\sqrt{\frac{36}{5}-\frac{36}{25}}$=$\frac{12}{5}$,
∵2<$\frac{12}{5}$<3,
∴点M在线段AT上,
即在线段AT上存在点M,使得OM⊥AM,M点的坐标为($\frac{12}{5}$,$\frac{6}{5}$).
点评 本题为反比例函数的综合应用,涉及相似三角形的判定和性质、全等三角形的判定和性质、圆的性质、勾股定理、等积法等知识.在(1)中证得△EPD∽△CPA是解题的关键,在(2)中构造全等三角形,求得ac=4是解题的关键,在(3)中求得A点坐标,再分别求得OM和ON的长是解题的关键.本题考查知识点较多,综合性较强,计算量较大,难度适中.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:填空题
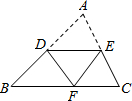 如图,△ABC的中位线DE=6cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为48cm2.
如图,△ABC的中位线DE=6cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为48cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
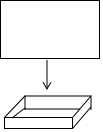 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
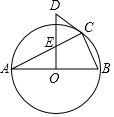 如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
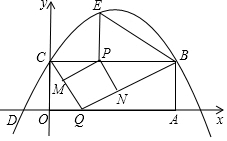 如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(-2,0),点P是线段CB上的动点,设CP=t(0<t<10).
如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(-2,0),点P是线段CB上的动点,设CP=t(0<t<10).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com