
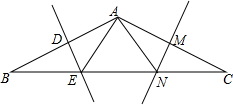
 在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.分析 (1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
解答 (1)解:∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+AN+EN=BE+EN+NC=BC=12;
(2)证明:∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∵EB=EA,NA=NC,
∴∠EAB=∠B=30°,∠NAC=∠C=30°,
∴∠AEN=∠EAB+∠B=60°,∠ANE=∠NAC+∠C=60°,
∴△AEN是等边三角形,
∴BE=EN=NC.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,∠BAC=120°.
如图,在△ABC中,AB=AC,∠BAC=120°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
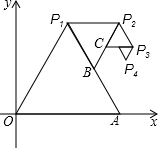 如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第五个正三角形中,不在第四个正三角形上的顶点P5的坐标是(2,$\frac{5\sqrt{3}}{8}$).
如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第五个正三角形中,不在第四个正三角形上的顶点P5的坐标是(2,$\frac{5\sqrt{3}}{8}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读理解:对于任意正实数a、b,∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,∴$a-2\sqrt{ab}+b$≥0,∴a+b≥$2\sqrt{ab}$只有当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,∴$a-2\sqrt{ab}+b$≥0,∴a+b≥$2\sqrt{ab}$只有当a=b时,等号成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com