练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

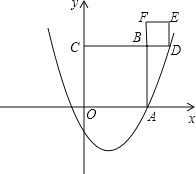
    【题目】如图，抛物线与x轴正半轴交于点A（3，0）．以OA为边在x轴上方作正方形OABC，延长CB交抛物线于点D，再以BD为边向上作正方形BDEF．则E的坐标是____．

    【答案】（1+，1+）．

    【解析】

    把点A（3，0）代入抛物线即可求得a的值，正方形OABC可得点C坐标，代入函数解析式求得点D坐标，可知点E横坐标，再利用正方形BDEF的性质得出点E纵坐标问题得解．

    解：把点A（3，0）代入抛物线，

    解得a＝；

    ∵四边形OABC为正方形，

    ∴点C的坐标为（0，3），点D的纵坐标为3，

    代入y＝x2﹣x﹣，

    解得x1＝1+，x2＝1﹣（不合题意，舍去），

    因此正方形BDEF的边长B为1+﹣3＝﹣2，

    所以AF＝3+﹣2＝1+，

    由此可以得出点E的坐标为（1+，1+）；

    故答案为：（1+，1+）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线与轴、轴分别交于点，，抛物线经过点，将点向右平移5个单位长度，得到点．

    （1）求点的坐标；

    （2）求抛物线的对称轴；

    （3）若抛物线与线段恰有一个公共点，结合函数图象，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷．某校数学兴趣小组设计了一份调查问卷，要求每人选且只选一种你最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

    （1）这次活动共调查了　 　人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为　 　；

    （2）将条形统计图补充完整．观察此图，支付方式的“众数”是“　 　”；

    （3）在一次购物中，小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图 ，是一元二次方程的两个实数根，且,抛物线的图象经过．

    （1）求抛物线的解析式；

    （2）设抛物线与轴的另一个交的为，抛物线的顶点为，求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

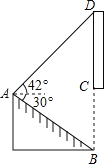
    【题目】2021年世界园艺博览会将在扬州枣林湾举办，有一块枣林湾博览会的直传牌CD竖立在路边，其中CB是支柱．小梅同学想计算出CD的长度．于是在A处测得支柱B处的俯角为30°．测得顶端D处的仰角为42°，同时测量出AB的长度是10m，BC的长度是6m．求宜传牌CD的长度（结果保留小数点后一位）．（参考数据：≈1.73，sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

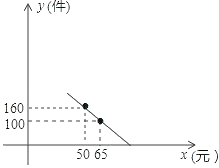
    【题目】某商场老板对一种新上市商品的销售情况进行记录，已知这种商品进价为每件 40 元，经过记录分析发现，当销售单价在 40 元至 90 元之间（含40 元和 90 元）时，每月的销售量 y（件）与销售单价 x（元）之间的关系可近似地看作一次函数，其图象如图所示．

    （1）求 y 与 x 的函数关系式．

    （2）设商场老板每月获得的利润为P（元），求 P 与 x 之间的函数关系式；并求出利润的最大时销售单价为多少元？

    （3）如果想要每月获得 2400 元的利润，那么销售单价应定为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，∠ACB=30°，将一块直角三角板的直角顶点P放在两对角线AC，BD的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别于边AB，BC所在的直线相交，交点分别为E，F．

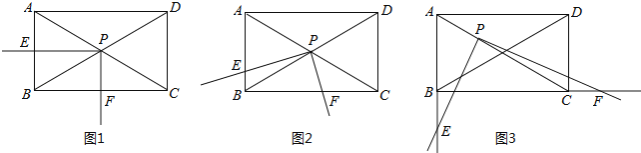
    （1）当PE⊥AB，PF⊥BC时，如图1，则的值为　 　；

    （2）现将三角板绕点P逆时针旋转α（0°＜α＜60°）角，如图2，求的值；

    （3）在（2）的基础上继续旋转，当60°＜α＜90°，且使AP：PC=1：2时，如图3，的值是否变化？证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一商品销售某种商品，平均每天可售出20件，每件盈利50元.为了扩大销售，增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.

    （1）若每件商品降价2元，则平均每天可售出______件；

    （2）当每件商品降价多少元时，该商品每天的销售利润为1600元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，顶点为（1，4）的抛物线与直线交于点A(2,2),直线与轴交于点B与轴交于点C

    (1)求的值及抛物线的解析式

    (2)P为抛物线上的点，点P关于直线AB的对称轴点在轴上，求点P的坐标

    (3)点D为轴上方抛物线上的一点，点E为轴上一点，以A 、B、E、D为顶点的四边为平行四边形时，直接写出点E的坐标。

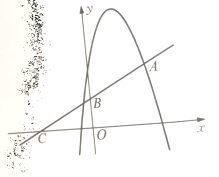
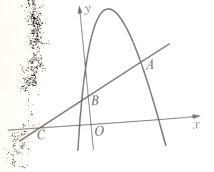
    查看答案和解析>>

    同步练习册答案