
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F,G.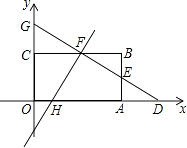
(1)求直线DE的函数关系式;
(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
【答案】
(1)
解:设直线DE的解析式为:y=kx+b,
∵顶点B的坐标为(6,4),E为AB的中点,
∴点E的坐标为:(6,2),
∵D(8,0),
∴ ![]() ,
,
解得: ![]() ,
,
∴直线DE的函数关系式为:y=﹣x+8
(2)
解:∵点F的纵坐标为4,且点F在直线DE上,
∴﹣x+8=4,
解得:x=4,
∴点F的坐标为;(4,4);
∵函数y=mx﹣2的图象经过点F,
∴4m﹣2=4,
解得:m= ![]()
(3)
解:由(2)得:直线FH的解析式为:y= ![]() x﹣2,
x﹣2,
∵ ![]() x﹣2=0,
x﹣2=0,
解得:x= ![]() ,
,
∴点H( ![]() ,0),
,0),
∵G是直线DE与y轴的交点,
∴点G(0,8),
∴OH= ![]() ,CF=4,OC=4,CG=OG﹣OC=4,
,CF=4,OC=4,CG=OG﹣OC=4,
∴S四边形OHFG=S梯形OHFC+S△CFG= ![]() ×(
×( ![]() +4)×4+
+4)×4+ ![]() ×4×4=18
×4×4=18 ![]()
【解析】(1)由顶点B的坐标为(6,4),E为AB的中点,可求得点E的坐标,又由过点D(8,0),利用待定系数法即可求得直线DE的函数关系式;(2)由(1)可求得点F的坐标,又由函数y=mx﹣2的图象经过点F,利用待定系数法即可求得m值;(3)首先可求得点H与G的坐标,即可求得CG,OC,CF,OH的长,然后由S四边形OHFG=S梯形OHFC+S△CFG , 求得答案.


科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣3|﹣5×(﹣ ![]() )+(﹣4);
)+(﹣4);
(2)(﹣2)2﹣4÷(﹣ ![]() )+(﹣1)2016;
)+(﹣1)2016;
(3)﹣14﹣ ![]() ×[3﹣(﹣3)2];
×[3﹣(﹣3)2];
(4)﹣81÷ ![]() ×
× ![]() ÷(﹣16).
÷(﹣16).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我们三个市参加中考的考生共约11万人,用科学记数法表示11万这个数是( )
A.1.1×103
B.1.1×104
C.1.1×105
D.1.1×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的“十六大”报告提出全面建设小康社会,加快推进社会主义现代化,力争国民经济总产值到2020年比2000年翻两翻,以每十年为基准计算,增长率为x,则( )
A. (1+x)2=2B. (1+x)2=4
C. (1+x)2+2(1+x)=4D. 1+2x=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在坐标平面内有下列三条直线:
①经过点(0,2)且平行于x轴的直线;
②直线y=2x﹣8;
③经过点(0,12)且平行于直线y=﹣2x的直线,
其中经过点(5,2)但不经过第三象限的直线共有( )
A.0条
B.1条
C.2条
D.3条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com