
 DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙.这时AB与CD′相交于点O,D′E′与AB相交于点F,连接AD′.
DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙.这时AB与CD′相交于点O,D′E′与AB相交于点F,连接AD′.
| 1 |
| 2 |
| 1 |
| 2 |
| OA2+OD′2 |
| 32+42 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:044
如图,把一副三角板如图甲放置,其中![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,
,![]() ,把三角板
,把三角板![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() 如图乙.这时
如图乙.这时![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1
)求(2
)求线段(3
)若把三角形
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙.这时AB与CD′相交于点O,D′E′与AB相交于点F,连接AD′.
DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙.这时AB与CD′相交于点O,D′E′与AB相交于点F,连接AD′.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,把一副三角板如图(1)放置,其中![]() ,斜边
,斜边![]() 把三角板DCE绕点C顺时针旋转15°得到
把三角板DCE绕点C顺时针旋转15°得到![]() 如图(2), 这时AB与
如图(2), 这时AB与![]() 相交于点
相交于点![]() ,
,![]() 与AB相交于点F。
与AB相交于点F。
(1)求![]() 的度数;
的度数;
(2)求线段![]() 的长;
的长;
(3)若把三角形![]() 绕着点C顺时针再旋转30°得到
绕着点C顺时针再旋转30°得到![]() ,这时点B在
,这时点B在![]() 的内部,外部,还是边上?证明你的判断。
的内部,外部,还是边上?证明你的判断。
 | 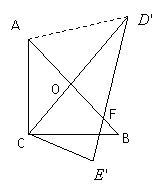 | ||
(1) (2)
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市丰台三中九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com