
如图,抛物线经过点A(1,0),B(5,0),C(0,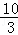 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边 形OEBF是以OB为对角线的平行四边形.
形OEBF是以OB为对角线的平行四边形.
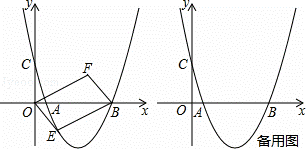
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
解:(1)设所求抛物线的解析式为y=ax2+bx+c,
∵抛物线经过点A(1,0),B(5,0),C(0,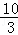 )三点,则由题意可得:
)三点,则由题意可得:
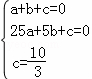 ,解得
,解得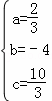 .
.
∴所求抛物线的解析式为:y=x2﹣4x+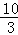 .
.
(2)∵点E(x,y)是抛物线上一动点,且在x轴下方,
∴y<0,
即﹣y>0,﹣y表示点E到OA的距离.
∵OB是平行四边形OEBF的对角线,
∴S=2S△OBE=2××OB•|y|=﹣5y=﹣5(x2﹣4x+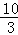 )=﹣
)=﹣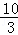 x2+20x﹣
x2+20x﹣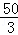 ,
,
∵S=﹣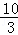 (x﹣3)2+
(x﹣3)2+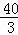
∴S与x之间的函数关系式为:S=﹣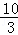 x2+20x﹣
x2+20x﹣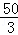 (1<x<5),S的最大值为
(1<x<5),S的最大值为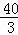 .
.
(3)∵当OB⊥EF,且OB=EF时,平行四边形OEBF是正方形,
∴此时点E坐标只能(,﹣),而坐标为(,﹣)点在抛物线上,
∴存在点E(,﹣),使平行四边形OEBF为正方形,
此时点F坐标为(,).


科目:初中数学 来源: 题型:
如图所示,已知二次函数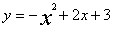 与坐标轴分别交于A、D、B三点,顶点为C。
与坐标轴分别交于A、D、B三点,顶点为C。
(1)求tan∠BAC
(2)在y轴上是否存在一点P,使得△DOP与△ABC相似,如果存在,求出点P的坐标,如果不存在,说明理由。
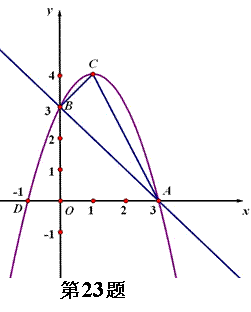 (3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)
(3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
数学课上,老师用多媒体给同学们放了由魔术界当红艺人刘谦表演的的神奇的障眼法“硬币穿玻璃”魔术,敏捷的身手、幽默的语言把同学们逗得乐不可支。看完后老师说:“今天我也来当一回魔术师给你们现场表演一个数学魔术。”说完便在黑板上画出下面两个图:
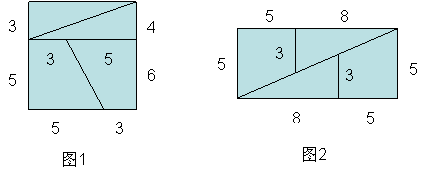

请你借助数学知识帮助同学们分析老师画的这两个图,通过计算验证说明图1到图2的拼接是否可行,若不行请说明理由,并画出正确的拼接图
查看答案和解析>>
科目:初中数学 来源: 题型:
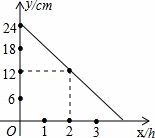
在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系中,点A的坐标为(﹣1,2),点C的坐标为(﹣3,0),将点C绕点A逆时针旋转90°,再向下平移3个单位,此时点C的对应点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
下列运算正确的是( )
|
| A. | a2+a3=a5 | B. | (﹣2a2)3=﹣6a6 | C. | (2a+1)(2a﹣1)=2a2﹣1 | D. | (2a3﹣a2)÷a2=2a﹣1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com