
【题目】如图1,已知点E为正方形ABCD对角线CA延长线上一点,过E点作EF⊥CB交其延长线于点F,且EF=4,AC=![]()
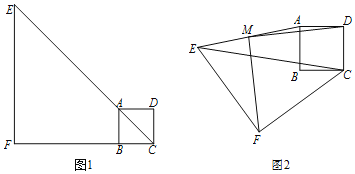
(1)如图1,连接BE,求线段BE的长;
(2)将等腰Rt△CEF绕C点旋转至如图2的位置,连接AE,M点为AE的中点,连接MD、MF,求MD与MF的关系;
(3)将△CEF绕C点旋转一周,请直接写出点M在这个过程中的运动路径长为 .
【答案】(1)5;(2)DM=MF,DM⊥MF.(3)4![]() π.
π.
【解析】
(1)连接BE,再求出BF的长,然后利用勾股定理进行解答即可;
(2)延长FM到P,使得MP=MF,连接PD、PF、PA,延长PA交CF于K.证明△PDF是等腰直角三角形即可完成解答;
(3)接AC,取AC的中点O,连接OM,由中位线定理可得OM=2![]() ,推出点M的运动轨迹是以O为圆心,2
,推出点M的运动轨迹是以O为圆心,2![]() 为半径的圆即可完成解答.
为半径的圆即可完成解答.
解:(1)如图1中,连接BE.
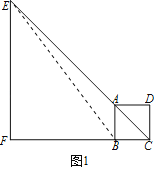
∵S四边形ABCD是正方形,
∴∠ACB=45°,AB=BC,∠ABC=90°,
∵AC=![]() ,
,
∴AB=BC=1,
∵EF⊥CF,
∴∠F=90°,
∴∠FCA=∠FAC=45°,
∴EF=FC=4,
∴FB=3,
∴BE=![]() =
=![]() =5.
=5.
(2)结论:MD=MF,MD⊥MF.
理由:延长FM到P,使得MP=MF,连接PD,PF,PA,延长PA交CF于K.
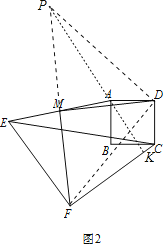
∵EM=MA,MF=MP,∠EMF=∠AMP,
∴△EMF≌△AMP(SAS),
∴PA=EF=CF,∠EFM=∠APM,
∴PK∥EF,
∵EF⊥CF,
∴PK⊥CF,
∴∠AKC=∠ADC=90°,
∴∠DAK+∠DCK=180°,
∵∠DAK+∠PAD=180°,
∴∠PAD=∠DCF,
∵CD=DC,
∴△PAD≌△FCD(SAS),
∴DP=DF,∠PDA=∠FDC,
∴∠PDF=∠ADC=90°,
∵PM=MF,
∴DM=MF=PM,DM⊥FM.
∴DM=MF,DM⊥MF.
(3)连接AC,取AC的中点O,连接OM.
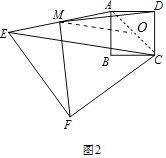
∵AM=ME,AO=OC,
∴OM=![]() EC,
EC,
∵EC=4![]() ,
,
∴OM=2![]() =定长,
=定长,
∴点M的运动轨迹是以O为圆心,2![]() 为半径的圆,
为半径的圆,
当△CEF绕C点旋转一周,M的轨迹为整个圆,
因此路径长为4![]() π,
π,
故答案为4![]() π.
π.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.

(1)请分别作出下图中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
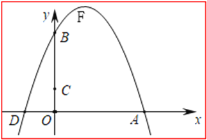
【题目】抛物线![]() 与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,
与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,![]()
(1)直接写出点B、A、F的坐标;
(2)设Q在该抛物线上,且![]() ,求点Q的坐标;
,求点Q的坐标;
(3)对大于1常数m,在x轴上是否存在点M,使得![]() ?若存在,求出点M坐标;若不存在,说明理由?
?若存在,求出点M坐标;若不存在,说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省南部的南宫山景区,为吸引游客组团来此旅游特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格70元/人
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于55元/人
(1)若某单位组织22名员工去南宫山景区旅游,则购买门票共需多少元?
(2)若某单位共支付南宫山景区门票费用1500元,试求该单位这次共有多少名员工去南宫山旅游.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(t,0),B(t+2,0).对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角点”.
(Ⅰ)当t=﹣1时,点C(0,1),判断点C是否为线段AB的“直角点”,并说明理由;
(Ⅱ)已知抛物线y=ax2+bx(a>0,b<0)的顶点为M,与x轴交于A(t,0),B(t+2,0),若点M为线段AB的“直角点”,求出此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
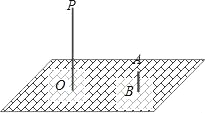
【题目】如图,晚上,小亮在广场上乘凉.图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出小亮在照明灯(P)照射下的影子;
(2)如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,正方形
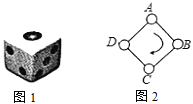
,如图2,正方形![]() 的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈
的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落在圈
个边长,落在圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从圈
,就从圈![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落得圈
个边长,落得圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.
(1)小贤随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(2)小南随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小贤落回到圈
,并指出他与小贤落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
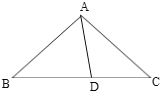
【题目】如图,在等腰△ABC中,AB=AC=4,BC=6点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com