
【题目】(1)分解因式![]()
(2)分解因式![]()
(3)计算![]()
(4)计算![]()
(5)解分式方程![]()
(6)解分式方程![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() (5)
(5)![]() ;(6)无解
;(6)无解
【解析】
(1)先提取公因式y,再利用完全平方公式分解;
(2) 先提取公因式7x,再利用平方差公式分解;
(3)先计算括号里,再将除法转化成乘法,再相乘即可;
(4)先化为同分母,再相加减即可;
(5)先将分式方程化成整式方程,再求解,最后验根即可;
(6) 先将分式方程化成整式方程,再求解,最后验根即可.
(1)![]()
=y(x2-2x+y2)
=y(x-y)2;
(2)![]()
=7x(x2-4)
=7x(x+2)(x-2);
(3)![]()
=![]()
=![]() ;
;
(4)![]()
=![]()
=![]()
=![]()
(5)![]()
2-x-1=x-3
2x=4
x=2
当x=2时,x-3≠0,所以x=2是方程的解;
(6)![]()
(x-2)2-16=(x+2)2
x2-4x+4-16=x2+4x+4
8x=-16
x=-2
当x=-2时,![]() =0,所以方程无解.
=0,所以方程无解.


科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.

(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动3.5秒时,求出点P的坐标;
(3)在移动过程中,若点P到x轴的距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 一同学利用直尺和圆规完成如下操作:
一同学利用直尺和圆规完成如下操作:
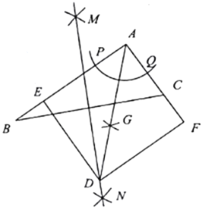
①以点![]() 为圆心,以适当的长为半径画弧,交
为圆心,以适当的长为半径画弧,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ;分别以点
;分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,
,
②分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,
,![]() 两点,直线
两点,直线![]() 交
交![]() 于
于![]() .
.
请你观察图形,根据操作结果解答下列问题:
(1)![]() 的度数为______;
的度数为______;
(2)作![]() 于
于![]() ,
,![]() 交
交![]() 的延长线于
的延长线于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
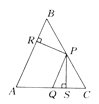
A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数y=k(x﹣ax﹣b),其中a≠b.
(1)若此二次函数图象经过点(0,k),试求a,b满足的关系式.
(2)若此二次函数和函数y=x2﹣2x的图象关于直线x=2对称,求该函数的表达式.
(3)若a+b=4,且当0≤x≤3时,有1≤y≤4,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(7,0),B(0,4),C(7,4),连接AC,BC得到矩形AOBC,点D在边BC上,将边OB沿OD折叠,点B的对应点为B′,若点B′到矩形较长两对边的距离之比为1:3,则BB′=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE平分∠BCD,交AB边于点E,EF∥BC,交CD于点F,点G是BC边的中点,连接GF,且∠1=∠2,CE与GF交于点M,过点M作MH⊥CD于点H.
(1)求证:四边形BCFE是菱形;
(2)若CH=1,求BC的长;
(3)求证:EM=FG+MH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在平面直角坐标系中,矩形OABC的顶点A(6,0),C(0,2![]() ),过y轴上的点D(0,3
),过y轴上的点D(0,3![]() ),作射线DM与x轴平行,点P,Q分别是射线DM与x轴正半轴上的动点,满足∠PQO=60°.设点P的横坐标为x(0≤x≤9),△OPQ与矩形的重叠部分的面积为y,则能大致反映y与x函数关系的图象是( )
),作射线DM与x轴平行,点P,Q分别是射线DM与x轴正半轴上的动点,满足∠PQO=60°.设点P的横坐标为x(0≤x≤9),△OPQ与矩形的重叠部分的面积为y,则能大致反映y与x函数关系的图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com