
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ//BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )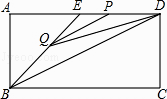
A.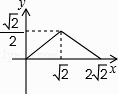
B.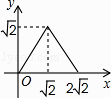
C.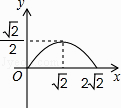
D.
【答案】C
【解析】解:∵∠ABE=45°,∠A=90°,
∴△ABE是等腰直角三角形,
∴AE=AB=2,BE= ![]() AB=2
AB=2 ![]() ,
,
∵BE=DE,PD=x,
∴PE=DE﹣PD=2 ![]() ﹣x,
﹣x,
∵PQ//BD,BE=DE,
∴QE=PE=2 ![]() ﹣x,
﹣x,
又∵△ABE是等腰直角三角形(已证),
∴点Q到AD的距离= ![]() (2
(2 ![]() ﹣x)=2﹣
﹣x)=2﹣ ![]() x,
x,
∴△PQD的面积y= ![]() x(2﹣
x(2﹣ ![]() x)=﹣
x)=﹣ ![]() (x2﹣2
(x2﹣2 ![]() x+2)=﹣
x+2)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
即y=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
纵观各选项,只有C选项符合.
故选:C.
判断出△ABE是等腰直角三角形,根据等腰直角三角形的性质求出AE、BE,然后表示出PE、QE,再求出点Q到AD的距离,然后根据三角形的面积公式表示出y与x的关系式,再根据二次函数图象解答.


科目:初中数学 来源: 题型:
【题目】(1)化简: ![]() (2)解方程:
(2)解方程:![]() .
.
【答案】(1) ![]() 或
或![]() ;(2)x=-2.
;(2)x=-2.
【解析】(1)先把括号内通分,再把除法转化为乘法,并把分子、分母分解因式约分化简;
(2)两边都乘以最简公分母2(x+3),把分式方程化为整式方程求解,求出x的值不要忘记检验.
(1)原式=![]() =
=![]() =
=![]() 或
或![]() ;
;
(2)解:去分母得:![]() ,
,
解得:x=﹣2,
经检验x=﹣2是分式方程的解,
∴原方程的解为x=﹣2
点睛:本题考查了分式的混合运算和解分式方程,熟练掌握分式的运算法则和解分式方程的方法是解答本题的关键.
【题型】解答题
【结束】
20
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中a= ;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为 ;
(4)若该辖区年龄在0~14岁的居民约有2400人,请估计该辖区居民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用 6000 元购进一批衬衫,以 60 元/件的价格出售,很快售完,然后又用 13500元购进同款衬衫,购进数量是第一次的 2 倍,购进的单价比上一次每件多 5 元,服装店 仍按原售价 60 元/件出售,并且全部售完.
(1)该服装店第一次购进衬衫多少件?
(2)将该服装店两次购进衬衫看作一笔生意,那么这笔生意是盈利还是亏损?求出盈利(或 亏损)多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两站相距240千米,从甲站开出一列慢车,速度为每小时80千米,从乙站开出一列快车,速度为每小时120千米.
(1)若两车同时开出,背向而行,则经过多长时间两车相距540千米?
(2)若两车同时开出,同向而行(快车在后),则经过多长时间快车可追上慢车?
(3)若两车同时开出,同向而行(慢车在后),则经过多长时间两车相距300千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 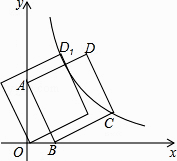
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com