
���� ��1������һ����ʽ�ǣ�x+b������2x-5����x+b��=2x2+2bx-5x-5b=2x2+��2b-5��x-5b=2x2+3x-k�����ݶ�Ӧ���ϵ����ȼ������b��k��ֵ��
��2������һ����ʽ�ǣ�3x+m�������ö���ʽ�ij˷����㷨��չ����Ȼ����ݶ�Ӧ���ϵ�������ʽ���m��a��ֵ��Ȼ��������ʽ���м��㼴�ɵý⣻
��3�����ڣ�x2��2-x3+mx2-2mx-2�ֽܷ����������ϵ���Ķ�����ʽ�Ļ������裨x2��2-x3+mx2-2mx-2=��x2+ax-1����x2+bx+2����x2+ax+1����x2+bx-2����չ�����ö�Ӧ���ϵ����ȼ��ɵó���
��� �⣺��1������һ����ʽ�ǣ�x+b������
��2x-5����x+b��=2x2+2bx-5x-5b=2x2+��2b-5��x-5b=2x2+3x-k��
��$\left\{\begin{array}{l}{2b-5=3}\\{-5b=-k}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=4}\\{k=20}\end{array}\right.$��
����һ����ʽ�ǣ�x+4��k=20��
��2������һ����ʽ�ǣ�3x+m������
��2x+a����3x+m��=6x2+��2m+3a��x+am=6x2+4ax+2��
��$\left\{\begin{array}{l}{2m+3a=4a}\\{am=2}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=2}\\{m=1}\end{array}\right.$��$\left\{\begin{array}{l}{a=-2}\\{m=-1}\end{array}\right.$��
��һ����ʽ��3x-1��a��ֵ��-2������������ȥ����
����һ����ʽ��3x+1��a��ֵ��2��
��3���ߣ�x2��2-x3+mx2-2mx-2�ֽܷ����������ϵ���Ķ�����ʽ�Ļ���
����裨x2��2-x3+mx2-2mx-2=��x2+ax-1����x2+bx+2����x2+ax+1����x2+bx-2����
�٣�x2+ax-1����x2+bx+2��=x4+��a+b��x3+��1+ab��x2+��2a-b��x-2��
��$\left\{\begin{array}{l}{a+b=-1}\\{1+ab=m}\\{2a-b=-2m}\end{array}\right.$��
���m=1��-$\frac{7}{4}$��
�ڣ�x2+ax+1����x2+bx-2��=x4+��a+b��x3+��ab-1��x2+��b-2a��x-2��
��$\left\{\begin{array}{l}{a+b=-1}\\{ab-1=m}\\{b-2a=-2m}\end{array}\right.$��
���m=-1��-$\frac{7}{4}$��
���Ͽɵã�m��ֵΪ1��$\frac{7}{4}$��-1��-$\frac{7}{4}$��
���� ���⿼������ʽ�ֽ�����壬��ȷ������ʽ�ֽ�����ʽ�ij˷���Ϊ�������ǹؼ���


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
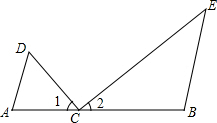 ��֪����ͼ��CΪ�߶�AB�ϳ��˵��������һ�㣬AD��BE���ҡ�D=��1����E=��2�����DCE�Ķ�����
��֪����ͼ��CΪ�߶�AB�ϳ��˵��������һ�㣬AD��BE���ҡ�D=��1����E=��2�����DCE�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com