
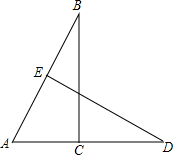
 如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )
如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )| A、∠AED>∠BED |
| B、∠AED<∠BED |
| C、∠AED=∠BED |
| D、无法确定 |
科目:初中数学 来源: 题型:
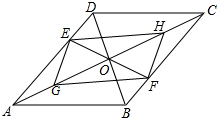 如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.
如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
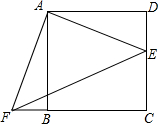 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.查看答案和解析>>
科目:初中数学 来源: 题型:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
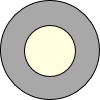 如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化
如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,绐正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为l的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2012次“移位”后,则他所处顶点的编号是
如图,绐正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为l的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2012次“移位”后,则他所处顶点的编号是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com