
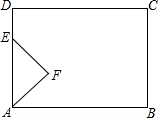
 如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).分析 (1)由矩形的性质和等腰直角三角形的性质得出FH=8cm,再由运动得出FH=t,即可;
(2)由等腰直角三角形的性质得出斜边上的高也是中线,根据三角形的中线把三角形AEF面积平分,判断出点F在CD上,即可;
(3)分三种情况先利用矩形和运动的特点显示出三角形高,底边和梯形的上下底,高,再利用三角形和梯形的面积公式求解;
(4)先判断出面积是17时,运动时间在3<t≤6内,再直接代入函数关系式中,即可.
解答 解:(1)如图1,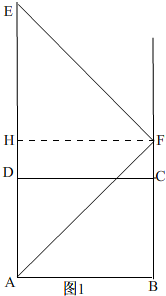
过点F作FH⊥AD于H,
在矩形ABCD中,AB=8cm,BC=6cm,∠BAD=90°,
∵点F落在射线BC上,
∴FH=8cm,
∴t=8s,
(2)如图2,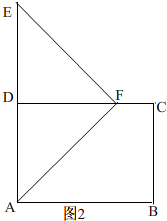
∵△AEF是等腰直角三角形,
∴AE边上的高线也是该边的中线,
∴点F在边CD上时,CD将△AEF的面积二等分,
∵FD是直角三角形的斜边的直线,
∴由运动知,FD=AD=6=t,
∴t=6s,
(3)当0<t≤3时,如图3,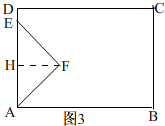
过点F作FH⊥AD,
由运动知,AE=2t,
∴FH=$\frac{1}{2}$AE=t,
∴S=$\frac{1}{2}$AE×FH=t2,
当3<t≤6时,如图4,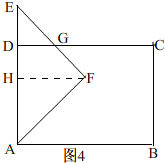
过点F作FH⊥AD,
由运动知,AE=2t,
∴DG=DE=2t-6,FH=t,DH=6-t,
∴S=$\frac{1}{2}$S△AEF+S梯形DHFG=$\frac{1}{2}$×$\frac{1}{2}$AE×FH+$\frac{1}{2}$(DG+FH)×DH=$\frac{1}{2}$×$\frac{1}{2}$×2t×t+$\frac{1}{2}$(2t-6+t)×(6-t)=-t2+12t-18,
当6<t≤8时,如图5,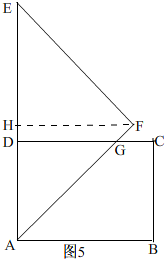
过点F作FH⊥AD,
∴DG=AD=6
∴S=$\frac{1}{2}$S△ADG=$\frac{1}{2}$AD×GD=18;
∴S=$\left\{\begin{array}{l}{{t}^{2}(0<t≤3)}\\{-{t}^{2}+12t-18(3<t≤6)}\\{18(6<t≤8)}\end{array}\right.$,
(4)由函数关系式知,S=17的运动时间在3<t≤6中,
将S=17代入S=-t2+12t-18中,
∴-t2+12t-18=17,
∴t=7(舍)或t=5
∴当S=17时,t的值为5s.
点评 此题是四边形综合题,主要考查了矩形的性质,等腰直角三角形的性质,梯形,三角形的面积公式,用运动时间表示线段是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
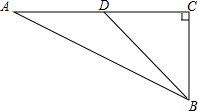 在Rt△ABC中,∠C=90°,AB=10$\sqrt{3}$,∠A=30°,求BD+$\frac{1}{2}$AD和2BD+$\sqrt{2}$AD的最小值.
在Rt△ABC中,∠C=90°,AB=10$\sqrt{3}$,∠A=30°,求BD+$\frac{1}{2}$AD和2BD+$\sqrt{2}$AD的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
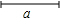 已知线段a,求作,△ABC,使AB=a,AC=BC=2a,画出图形后,测量一下∠CAB与∠CBA,猜想∠CAB与∠CBA的关系,你能说明你发现的结论吗?
已知线段a,求作,△ABC,使AB=a,AC=BC=2a,画出图形后,测量一下∠CAB与∠CBA,猜想∠CAB与∠CBA的关系,你能说明你发现的结论吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+2-2x+1 | B. | 3x+2-4x+1 | C. | 3x+2-4x-2 | D. | 3x+2-4x+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com