
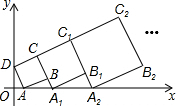
 在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032.
在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032. 分析 根据相似三角形的判定原理,得出△AA1B∽△A1A2B1,继而得知∠BAA1=∠B1A1A2;利用勾股定理计算出正方形的边长;最后利用正方形的面积公式计算第一个正方形的面积,从中找出规律,进而可求出第n个正方形的面积.
解答 解:设正方形的面积分别为S1,S2…,Sn,
根据题意,得:AD∥BC∥C1A2∥C2B2,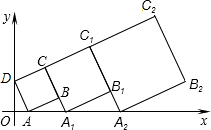
∴∠BAA1=∠B1A1A2=∠B2A2x(同位角相等).
∵∠ABA1=∠A1B1A2=∠A2B2x=90°,
∴△BAA1∽△B1A1A2,
在直角△ADO中,根据勾股定理,得:AD=$\sqrt{5}$,tan∠ADO=$\frac{OA}{OD}$=$\frac{1}{2}$,
∵tan∠BAA1=$\frac{B{A}_{1}}{AB}$=tan∠ADO,
∴BA1=$\frac{1}{2}$AB=$\frac{\sqrt{5}}{2}$,
∴CA1=$\sqrt{5}$+$\frac{\sqrt{5}}{2}$,
同理,得:C1A2=($\sqrt{5}$+$\frac{\sqrt{5}}{2}$)×(1+$\frac{1}{2}$),
由正方形的面积公式,得:S1=($\sqrt{5}$)2=5,
S2=($\sqrt{5}$)2×(1+$\frac{1}{2}$)2,
S3=($\sqrt{5}$)2×(1+$\frac{1}{2}$)4=5×($\frac{3}{2}$)4,
由此,可得S2017=($\sqrt{5}$)2×(1+$\frac{1}{2}$)2×2016=5×($\frac{3}{2}$)4032.
故答案为:5×($\frac{3}{2}$)4032.
点评 本题考查了正方形的性质,相似三角形的性质和判定,勾股定理的应用,解此题的关键是根据计算的结果得出规律,题目比较好,但是一道比较容易出错的题目.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
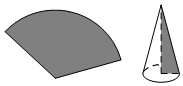
| A. | 3 cm | B. | 2$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
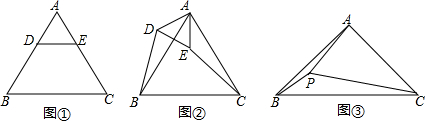
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com