
����Ŀ����ͼ1����![]() �ľŸ�����������
�ľŸ�����������![]() �����֣� ��ÿ�С�ÿ�м�ÿ���Խ��ߵ�
�����֣� ��ÿ�С�ÿ�м�ÿ���Խ��ߵ�![]() ������֮�Ͷ����ʱ�����ǰ�����ͼ��֮Ϊ�Ź���λͼ:
������֮�Ͷ����ʱ�����ǰ�����ͼ��֮Ϊ�Ź���λͼ:
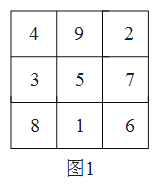
��1����![]() ����
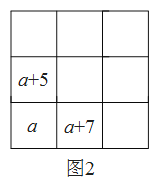
����![]() ����Ҳ�ܹ��ɾŹ���λͼ�� ���ʱÿ�С�ÿ�м�ÿ���Խ��ߵ�
����Ҳ�ܹ��ɾŹ���λͼ�� ���ʱÿ�С�ÿ�м�ÿ���Խ��ߵ�![]() ������֮�Ͷ�Ϊ ��
������֮�Ͷ�Ϊ ��
��2����ͼ2.�����žŹ���λͼ�У�ֻ������![]() �������뽫ʣ���
�������뽫ʣ���![]() ����ֱ�������2�У�(�ú�
����ֱ�������2�У�(�ú�![]() �Ĵ���ʽ�ֱ��ʾ��
�Ĵ���ʽ�ֱ��ʾ��![]() ����)
����)
��3����ͼ3�������žŹ���λͼ�У�ֻ������![]() ����������������Ͻǡ�
����������������Ͻǡ�![]() ������ʾ����ֵ.
������ʾ����ֵ.

���𰸡���1��6����2�������������3��1.
��������
��1�����������֪������2�϶����м�λ�ã������������ӵ���֮��Ϊ4�����ɵõ��𰸣�
��2����ͼ��֪����![]() ��9�����������������ݹ��ɣ����ɵõ��𰸣�
��9�����������������ݹ��ɣ����ɵõ��𰸣�
��3�������Ͻǡ�![]() ������ʾ����ֵΪ
������ʾ����ֵΪ![]() ����ո�����Ӧλ�õ���Ϊ
����ո�����Ӧλ�õ���Ϊ![]() ��Ȼ�����ÿ�С�ÿ�С�ÿ�Խ��ߵĺ���ȣ����������.
��Ȼ�����ÿ�С�ÿ�С�ÿ�Խ��ߵĺ���ȣ����������.
�⣺��1����![]() ����9�����У�
����9������
��2���м䣬�����������ӵ���֮��Ϊ4��
���ʱÿ�С�ÿ�м�ÿ���Խ��ߵ�![]() ������֮�Ͷ�Ϊ��
������֮�Ͷ�Ϊ��![]() ��
��
�ʴ�Ϊ��6.
��2����![]() ��9�����������������м����Ϊ
��9�����������������м����Ϊ![]() ��
��
�����������ͼ��

��3����ͼ�������Ͻǡ�![]() ������ʾ����ֵΪ
������ʾ����ֵΪ![]() ����ո�����Ӧλ�õ���Ϊ
����ո�����Ӧλ�õ���Ϊ![]() ��
��

������ɵã�![]() ��
��
�ɵã�![]() ��
��
��![]() ��
��
��ã�![]() .
.
�����Ͻǡ�![]() ������ʾ����ֵΪ1.
������ʾ����ֵΪ1.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x��ֱ���A��1��0����B��-5��0�����㣮
��1���������ߵĽ���ʽ��
��2���ڵ�һ������ȡһ��C����CD��ֱx���ڵ�D������AC����AD=5��CD=8����Rt��ACD��x������ƽ��m����λ������C������������ʱ����m��ֵ��
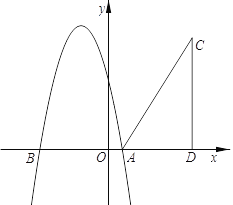
��3���ڣ�2���������£�����C��һ�������������ϼ�Ϊ��E����P�������߶Գ�����һ�㣮��̽���������������Ƿ���ڵ�Q��ʹ�Ե�B��E��P��QΪ������ı�����ƽ���ı��Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Ծ��꼶ȫ��ѧ��������һ��ѧҵˮƽ���ԣ��ɼ�������ΪA��B��C��D�ĸ��ȼ���A��B��C��D�ֱ�������㡢���á��ϸ��ϸ�У�Ӿ��꼶ѧ���������ȡ��һ����ѧ���ijɼ������Ƴ����²�������ͳ��ͼ���������ͳ��ͼ�ṩ����Ϣ����������⣻
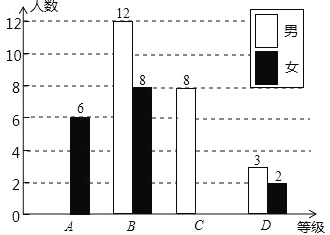
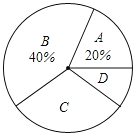
��1�����ε����У�һ����ȡ���� ����ѧ���ijɼ���
��2�������������ͳ��ͼ����������д������ͳ��ͼ�еȼ�C�İٷֱ��� ����
��3�����ȼ�D��5��ѧ���ijɼ�����λ���֣��ֱ���55��48��57��51��55������5�����ݵ���λ������ ���֣��������� ���֣�
��4�������У���꼶����500��ѧ�����Թ�������β����гɼ��ﵽ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD���ܳ�Ϊ36���Խ���AC��BD�ཻ�ڵ�O����E��CD���е㣬BD=12�����DOE���ܳ�Ϊ��������
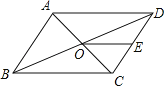
A. 15 B. 18 C. 21 D. 24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ��������÷��̽��ʵ�����������о������������������ᵽ��ôһ���������⾮�����⣺�����⾮�����������۲�֮�������ijߣ����������۲�֮������һ�ߣ���������������Σ�
����������˼�ǣ������Ӳ���ˮ����ȣ�����������۳����ȷݣ���ôÿ�ȷݾ��������ijߣ�����������۳��ĵȷݣ���ôÿ�ȷݾ�������һ�ߣ��������;�������ٳߣ����辮��Ϊx�ߣ�����⾮��ķ�����ȷ���ǣ�������
A.3��x+4����4��x+1��B.3x+4��4x+1
C.![]() x+4��
x+4��![]() x+1D.
x+1D.![]() x��4��
x��4��![]() x��1
x��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ķ���
�ķ���![]() .
.
��1�����ⷽ�̣��жϷ��̵ĸ��������
��2����![]() ������������
Ϊ���������Σ���![]() ,�����������Ƿ���
,�����������Ƿ���![]() �� ����������������ε��ܳ�.
�� ����������������ε��ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�2014��ij����10�������С�Сѧ��50���ܳɼ�������������Ŵ�������ѧ��Ⱥ���и���ȡ��10%��ѧ�����м�⣬�����������ݣ������2010�����������õ�����ͳ��ͼ��
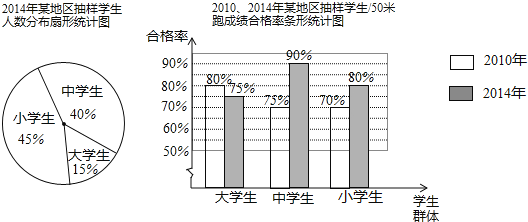
��1�����μ���ȡ�˴��С�Сѧ������ ����������Сѧ���� ������
��2�����ݳ����Ľ��������2014��õ���10�������С�Сѧ���У�50���ܳɼ��ϸ����ѧ������Ϊ�� ������
��3���Ƚ�2010����2014�����ѧ��50���ܳɼ��ϸ��������д��һ����ȷ�Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������C: y=ax2+bx+c��a��0����ֱ��l��y=kx+d��k��0��������y����һ��P����������C�Ķ���Q��ֱ��l�ϣ���ô�ƴ�ֱ��l���������C���С�һ��һ·����ϵ�����ֱ��y=mx+1��������y=x2-2x+n���С�һ��һ·����ϵ����ôm+n=_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪
��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪![]() ��
��![]() ��
��
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() �������ߵĶԳ������Ƿ���ڵ�P��ʹ
�������ߵĶԳ������Ƿ���ڵ�P��ʹ![]() ����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
![]() ��Eʱ�߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ��
��Eʱ�߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ��![]() �����������
�����������![]() ������������ʱE������꣮
������������ʱE������꣮

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com