
分析 先根据分母有理化的计算法则化简x、y,然后代入求值.
解答 解:x=$\frac{2+\sqrt{3}}{2-\sqrt{3}}$=(2+$\sqrt{3}$)2=7+4$\sqrt{3}$,y=$\frac{2-\sqrt{3}}{2+\sqrt{3}}$=(2-$\sqrt{3}$)2=7-4$\sqrt{3}$,
所以x+y=14,xy=1,
所以x3+y3=(x+y)(x2-xy+y2)
=(x+y)[(x+y)2-3xy]
=14×(142-3×1)
=2702.
点评 本题考查了二次根式的化简求值,根据题意得到“x+y=14,xy=1”和对所求代数式的变形是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,矩形OABC中,OA=4,OC=8,点D是线段OB的中点,点P从点A出发,以每秒1个单位的速度沿射线AO作匀速运动,点Q从点O出发,以每秒2个单位的速度沿x轴正半轴作匀速运动,P,Q同时出发,设运动的时间为t.
如图,矩形OABC中,OA=4,OC=8,点D是线段OB的中点,点P从点A出发,以每秒1个单位的速度沿射线AO作匀速运动,点Q从点O出发,以每秒2个单位的速度沿x轴正半轴作匀速运动,P,Q同时出发,设运动的时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,E为线段AB上一点,EC∥AD,DE∥BC,若S△EBC=1,S△ADE=3,则$\frac{AD}{EC}$=$\sqrt{3}$.
如图,E为线段AB上一点,EC∥AD,DE∥BC,若S△EBC=1,S△ADE=3,则$\frac{AD}{EC}$=$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
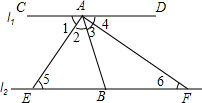 如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.
如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 图中是德国现代建筑师丹尼尔•里伯斯金设计的“时间迷宫”挂钟,它直观地表达出了设计师对时间的理解:时间是迷宫一般的存在--“若干抽象的连接和颇具玩味的互动”.在挂钟所在平面内,通过测量、画图等操作方式判断:AB,CD所在直线的位置关系是相交(填“相交”或“平行”),图中∠1与∠2的大小关系是∠1>∠2.(填“>”或“=”或“<”)
图中是德国现代建筑师丹尼尔•里伯斯金设计的“时间迷宫”挂钟,它直观地表达出了设计师对时间的理解:时间是迷宫一般的存在--“若干抽象的连接和颇具玩味的互动”.在挂钟所在平面内,通过测量、画图等操作方式判断:AB,CD所在直线的位置关系是相交(填“相交”或“平行”),图中∠1与∠2的大小关系是∠1>∠2.(填“>”或“=”或“<”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com