
【题目】如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 . 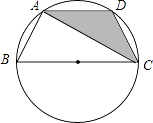
【答案】![]()
【解析】解:设圆心为O,连接OA、OD. 
∵AD∥BC,AC平分∠BCD,∠ADC=120°,
∴∠BCD=60°,
∵AC平分∠BCD,
∴∠ACD=30°,
∴∠AOD=2∠ACD=60°,∠OAC=∠ACO=30°.
∴∠BAC=90°,
∴BC是直径,
又∵OA=OD=OB=OC,
则△AOD、△AOB、△COD都是等边三角形.
∴AB=AD=CD.
又∵四边形ABCD的周长为10cm,
∴OB=OC=AB=AD=DC=2(cm).
∴阴影部分的面积=S梯形﹣S△ABC= ![]() (2+4)×
(2+4)× ![]() ﹣
﹣ ![]() ×4×
×4× ![]() =3
=3 ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
故答案为 ![]() .
.
连接OA、OD,则阴影部分的面积等于梯形的面积减去三角形的面积.根据题目中的条件不难发现等边三角形AOD、AOB、COD,从而求解.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F. 
(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B.C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①探究BD与CF之间的位置关系,并说明理由;
②当AB= ![]() ,AD=
,AD= ![]() +1时,求线段DH的长.
+1时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,E是AD的中点,将△CDE沿CE折叠后,点A和点D恰好重合,若菱形ABCD的面积为4 ![]() ,则菱形ABCD的周长是( )
,则菱形ABCD的周长是( ) 
A.8 ![]()
B.16 ![]()
C.8 ![]()
D.16 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+4ax+b与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC. 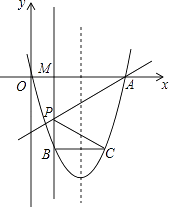
(1)a= ![]() 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图a<﹣1时,若AP⊥PC,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线 ![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.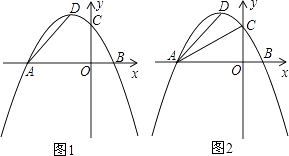
(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知式子M=(a+5)x3+7x2﹣2x+5是关于x的二次多项式,且二次项系数为b,数轴上A、B两点所对应的数分别是a和b.
(1)则a= ,b= .A、B两点之间的距离= ;
(2)有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点P所对应的有理数.
(3)在(2)的条件下,点P会不会在某次运动时恰好到达某一位置,使点P到点B的距离是点P到点A的距离的3倍?若可能请求出此时点P的位置,并直接指出是第几次运动,若不可能请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣7﹣5.
(2)(﹣15)﹣(﹣9)
(3)(﹣5)×(﹣7)+20÷(﹣4)
(4)(![]() )×(﹣36)
)×(﹣36)
(5)﹣81÷![]() ×
×![]() ÷(﹣16)
÷(﹣16)
(6)5![]() ﹣(﹣2
﹣(﹣2![]() )+(﹣3
)+(﹣3![]() )﹣(+4
)﹣(+4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 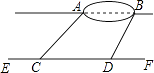
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com