
【题目】问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
(应用):
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
(拓展):
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)已知E(2,0),若F(﹣1,﹣2),求d(E,F);
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,求t的值;
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,求d(P,Q).

【答案】【应用】:(1)3;(2)(1,2)或(1,﹣2);【拓展】:(1)5;(2)t=±2;(3)d(P,Q)的值为4或8.
【解析】
(1)根据若y1=y2,则AB∥x轴,且线段AB的长度为|x1-x2|,代入数据即可得出结论;
(2)由CD∥y轴,可设点D的坐标为(1,m),根据CD=2即可得出|0-m|=2,解之即可得出结论;
【拓展】:(1)根据两点之间的折线距离公式,代入数据即可得出结论;
(2)根据两点之间的折线距离公式结合d(E,H)=3,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)由点Q在x轴上,可设点Q的坐标为(x,0),根据三角形的面积公式结合三角形OPQ的面积为3即可求出x的值,再利用两点之间的折线距离公式即可得出结论.
解:【应用】:
(1)AB的长度为|﹣1﹣2|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).
【拓展】
:
(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.
故答案为:5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|2﹣1|+|0﹣t|=3,
解得:t=±2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴![]() |x|×3=3,解得:x=±2.
|x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;
当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8
综上所述,d(P,Q)的值为4或8.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
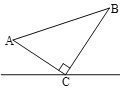
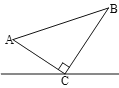
【题目】如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
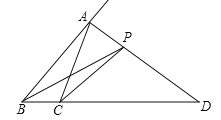
A.a>b B.a=b C.a<b D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
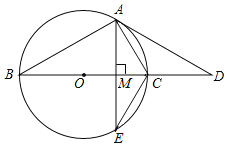
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3x2+x+2,B=﹣3x2+9x+6.
(1)求2A﹣![]() B;
B;
(2)若2A﹣![]() B与
B与![]() 互为相反数,求C的表达式;
互为相反数,求C的表达式;
(3)在(2)的条件下,若x=2是C=2x+7a的解,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:
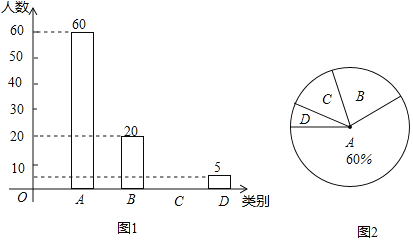
(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:
少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学是神秘奇妙的,数与字母有着密切的联系,字母可以表示数,数可以赋予字母其值,以下是某同学参加校庆举办的“越战越勇”活动的一道思考题,请同学们帮他完成,
(1)填表:
|
| |
用代数式表示 |
| |
|
| |
| ||
|
根据表中计算结果,你发现了什么等式?请写出这个等式
(2)利用(1)中发现的结论,计算![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
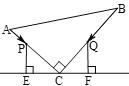
【题目】如图所示,△ABC中,∠ACB=90°,AC=6cm,BC =8cm.点P从A点出发,沿![]() 路径向终点B运动,点Q从B点出发,沿
路径向终点B运动,点Q从B点出发,沿![]() 路径向终点A运动.点P 和Q分别
路径向终点A运动.点P 和Q分别![]() 和
和![]() 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com