
【题目】如图,△ABC中,AB=AC,

(1)请你利用直尺和圆规完成如下操作:
①作△ABC的角平分线AD;
②作边AB的垂直平分线EF,EF与AD相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(2)线段PA,PB,PC之间的数量关系是 ;请说明理由.
(3)若∠ABC=70°,求∠BPC的度数.
【答案】(1)见解析;(2)PA=PB=PC,理由见解析;(3)80°.
【解析】
(1)利用基本作图作角平分线AD和AB的垂直平分线,它们相交于P点;
(2)根据线段的垂直平分线的性质可得:PA=PB=PC;
(3)根据等腰三角形的性质得:∠ABC=∠ACB=70°,由三角形的内角和得:∠BAC=180°-2×70°=40°,由角平分线定义得:∠BAD=∠CAD=20°,最后利用三角形外角的性质可得结论.
解:(1)如图,AD、EF 、点P为所作;
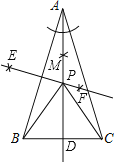
(2)PA=PB=PC,理由:
∵AB=AC,AD平分∠BAC,
∴AD是BC的垂直平分线,
∴PB=PC,
∵EP是AB的垂直平分线,
∴PA=PB,
∴PA=PB=PC;
故答案为:PA=PB=PC;
(3)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°-2×70°=40°,
∵AM平分∠BAC,
∴∠BAD=∠CAD=20°,
∵PA=PB=PC,
∴∠ABP=∠BAP=∠ACP=20°,
∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=50°,BD,CE是∠ABC,∠ACB的平分线,则∠BOC的度数为( )

A.105°B.115°C.125°D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张三角形纸片ABC,其中∠BAC=60°,BC=6,点D是BC边上一动点,将BD,CD翻折使得B′,C′分别落在AB,AC边上,(B与B′,C与C′分别对应),点D从点B运动至点C,△B′C′D面积的大小变化情况是( )

A. 一直减小 B. 一直不变 C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
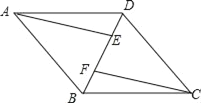
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
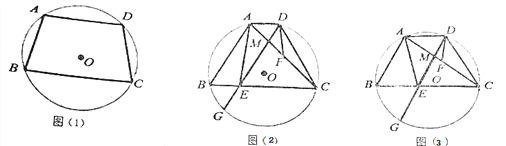
【题目】如图,四边形ABCD是⊙O的内接四边形,AB=CD.
(1)如图(1),求证:AD∥BC;
(2)如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF;
(3)在(2)的条件下,若DG平分∠ADC,GE=5![]() ,tan∠ADF=4
,tan∠ADF=4![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
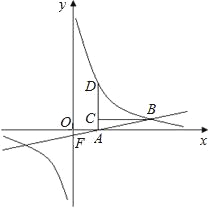
【题目】如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
(1)求该双曲线的解析式;
(2)求△OFA的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com