
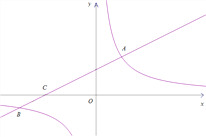
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线![]() 的解析式;
的解析式;
(2)若点P在x轴上,且![]() ,求点P的坐 标(直接写出结果).
,求点P的坐 标(直接写出结果).
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】某公园元旦期间,前往参观的人非常多.这期间某一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.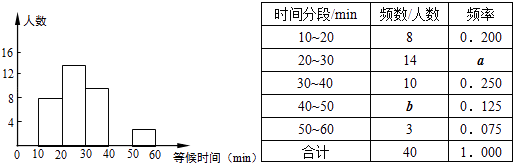
(1)这里采用的调查方式是(填“普查”或“抽样调查”),样本容量是;
(2)表中a= , b= , 并请补全频数分布直方图;
(3)在调查人数里,若将时间分段内的人数绘成扇形统计图,则“40~50”的圆心角的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于 ![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( ) 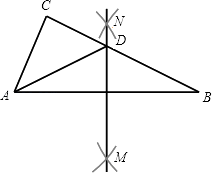
A.7
B.14
C.17
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出△A1B1C1各顶点坐标;
(2)将△ABC向左平移1个单位,作出平移后的△A2B2C2 , 并写出△A2B2C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△AOB的三个顶点A,O,B都在格点上.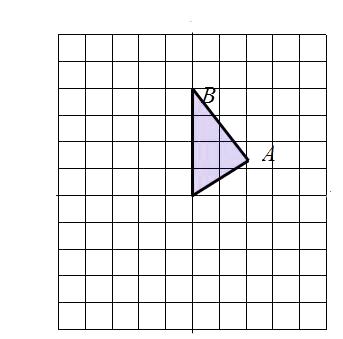
(1)画出△AOB关于点O成中心对称的三角形;
(2)画出△AOB绕点O逆时针旋转90后得到的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90度.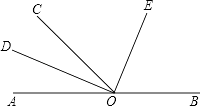
(1)请你数一数,图中有多少个角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把下面的频数分布表和频数分布直方图补充完整;
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 0.24 | |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | |
25<x≤30 | 2 | 0.04 |
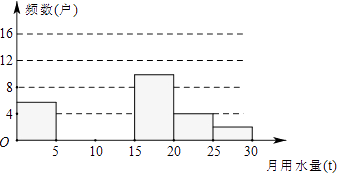
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F在OD上一点,且∠1=∠A. 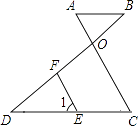
(1)求证:FE∥OC;
(2)若∠DFE=70°,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com