
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
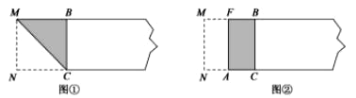
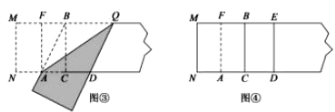
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
【答案】(1)![]() ;(2)见解析;(3) 见解析; (4) 见解析.
;(2)见解析;(3) 见解析; (4) 见解析.
【解析】(1)由勾股定理计算即可;
(2)根据菱形的判定方法即可判断;
(3)根据黄金矩形的定义即可判断;
(4)如图④﹣1中,在矩形BCDE上添加线段GH,使得四边形GCDH为正方形,此时四边形BGHE为所求是黄金矩形.
(1)如图3中.在Rt△ABC中,AB=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
(2)结论:四边形BADQ是菱形.理由如下:
如图③中,∵四边形ACBF是矩形,∴BQ∥AD.
∵AB∥DQ,∴四边形ABQD是平行四边形,由翻折可知:AB=AD,∴四边形ABQD是菱形.
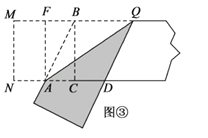
(3)如图④中,黄金矩形有矩形BCDE,矩形MNDE.
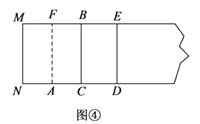
∵AD=![]() .AN=AC=1,CD=AD﹣AC=
.AN=AC=1,CD=AD﹣AC=![]() ﹣1.
﹣1.
∵BC=2,∴![]() =
=![]() ,∴矩形BCDE是黄金矩形.
,∴矩形BCDE是黄金矩形.
∵![]() =
=![]() =
=![]() ,∴矩形MNDE是黄金矩形.
,∴矩形MNDE是黄金矩形.
(4)如图④﹣1中,在矩形BCDE上添加线段GH,使得四边形GCDH为正方形,此时四边形BGHE为所求是黄金矩形.
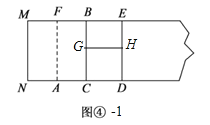
长GH=![]() ﹣1,宽HE=3﹣
﹣1,宽HE=3﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
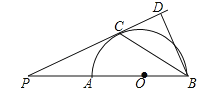
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DF分别交AB、AC于点E、G,连解FG,下列结论:(1)∠AGD=112.5°;(2)E为AB中点;(3)S△AGD=S△OCD;(4)正边形AEFG是菱形;(5)BE=2OG,其中正确结论的个是( )
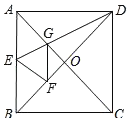
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
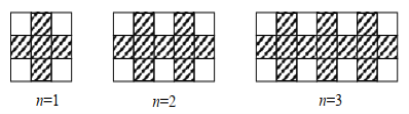
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料.
在数学课上,老师请同学思考如下问题:
已知:如图①,在△ABC中,∠A=90°.

图①
求作:⊙P,使得点P在边AC上,且⊙P与AB,BC都相切.
小轩的主要作法如下:
如图②,

图②
(1)作∠ABC的平分线BF,与AC交于点P;
(2)以P为圆心,AP长为半径作⊙P,则⊙P即为所求.
老师说:“小轩的作法正确.”
请回答:⊙P与BC相切的依据是 ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人准备玩传球游戏.规则是:第1次传球从甲开始,甲先将球随机传给乙、丙两人中的一个人,再由接到球的人随机传给其他两人中的一个人…如此反复.
(1)若传球1次,球在乙手中的概率为 ;
(2)若传球3次,求球在甲手中的概率(用树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松桃孟溪火车站一检修员某天乘一辆检修车在笔直的铁轨上来回检修,规定向东为正,从车站出发到收工时,行走记录为(单位:千米):+15,-2,-5,-1,+10,-3,-2,-12,+4,+6.
⑴计算收工时,检修员在车站的哪一边,此时,距车站多远?
⑵若汽车每千米耗油0.1升,且汽油的价格为每升6.8元,求这一天检修员从出发到收工时所耗油费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com