
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
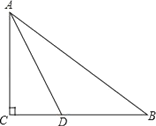
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD=2![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
【答案】(1)见解析;(2)见解析;(3)![]() π
π
【解析】
(1)作AD的垂直平分线交AB于点O,以OA为半径画圆O分别交AB、AC于点E、F,则圆O即为所求;
(2)连接OD,得到OD=OA,根据等腰三角形的性质得到∠OAD=∠ODA,等量代换得到∠ODA=∠CAD,根据平行线的判定定理可得,OD∥AC,再根据平行线的性质可求证结论;
(3)连接DE,根据圆周角定理得到∠ADE=90°,根据三角形内角和定理得到∠AOD=120°,根据三角函数的定义得到AE=![]() ,再根据弧长公式可得结论.
,再根据弧长公式可得结论.
(1)解:如图所示,
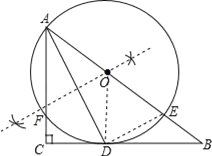
(2)证明:连结OD,则OD=OA,
∴∠OAD=∠ODA,
∵∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
即BC⊥OD,
∵BC经过半径OD的外端
∴BC与⊙O相切;
(3)解:连接DE,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠OAD=∠ODA=∠CAD=30°,
∴∠AOD=120°,
在Rt△ADE中,
AE=![]() =
= ![]() =4,
=4,
∴⊙O的半径=2,
∴劣弧AD的长=![]() =
=![]() π.
π.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
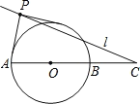
【题目】如图,已知⊙O 的半径长为2,点C为直径AB的延长线上一点,且BC=2.过点C任作一条直线l.若直线l上总存在点P,使得过点P所作的⊙O 的两条切线互相垂直,则∠ACP的最大值等于__________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
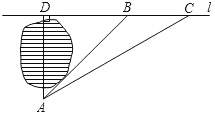
【题目】如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=100m.请你帮小明计算他家到公路l的距离AD的长度?(精确到1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对“隔离直线”给出如下定义:点
中,对“隔离直线”给出如下定义:点![]() 是图形
是图形![]() 上的任意一点,点
上的任意一点,点![]() 是图形
是图形![]() 上的任意一点,若存在直线
上的任意一点,若存在直线![]() :
:![]() 满足
满足![]() 且
且![]() ,则称直线
,则称直线![]() :
:![]() 是图形
是图形![]() 与
与![]() 的“隔离直线”,如图
的“隔离直线”,如图![]() ,直线
,直线![]() :
:![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的一条“隔离直线”.
的一条“隔离直线”.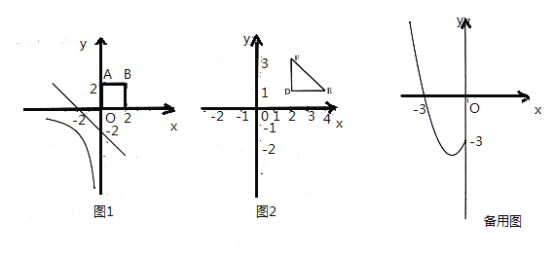
(1)在直线①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是图
中,是图![]() 函数
函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”的为 .
的“隔离直线”的为 .
(2)如图![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的两腰分别与坐标轴平行,直角顶点
的两腰分别与坐标轴平行,直角顶点![]() 的坐标是
的坐标是![]() ,⊙O的半径为
,⊙O的半径为![]() ,是否存在
,是否存在![]() 与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
(3)正方形![]() 的一边在
的一边在![]() 轴上,其它三边都在
轴上,其它三边都在![]() 轴的左侧,点
轴的左侧,点![]() 是此正方形的中心,若存在直线
是此正方形的中心,若存在直线![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”,请直接写出
的“隔离直线”,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,我们将横、纵坐标都是整数的点称为“整点”.若抛物线y=ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”,则a的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)M{(﹣2)2,22,﹣22}=_____;
(2)若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有3个相同的小球,将3个小球分别标示号码1、2、3,每次从盒子里随机取出1个小球且取后放回,预计取球10次.若规定每次取球时,取出的号码即为得分,则前八次的取球得分情况如下表所示
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
(1)设第1次至第8次取球得分的平均数为![]() ,求
,求![]() 的值:
的值:
(2)求事件“第9次和第10次取球得分的平均数等于![]() ”发生的概率;(列表法或树状图)
”发生的概率;(列表法或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若整数a使关于x的分式方程![]() 的解为整数,且使关于y的不等式组
的解为整数,且使关于y的不等式组![]() 有解,且最多有4个整数解,则符合条件的所有整数a的和为( )
有解,且最多有4个整数解,则符合条件的所有整数a的和为( )
A.﹣3B.﹣8C.﹣13D.﹣17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com